The Shunting Yard Algorithm
@beng showed us his BASIC interpreter for which he eventually had to implement the shunting yard algorithm. It was written because he wanted to run old BASIC games like traitor's castle.
It needed to handle BASIC weirdness like arbitrary gotos, ubiquitous global state. Initially it used a eval-based strategy, where each line was converted into a ruby method that more-or-less eval'd the line contents in a specific context.
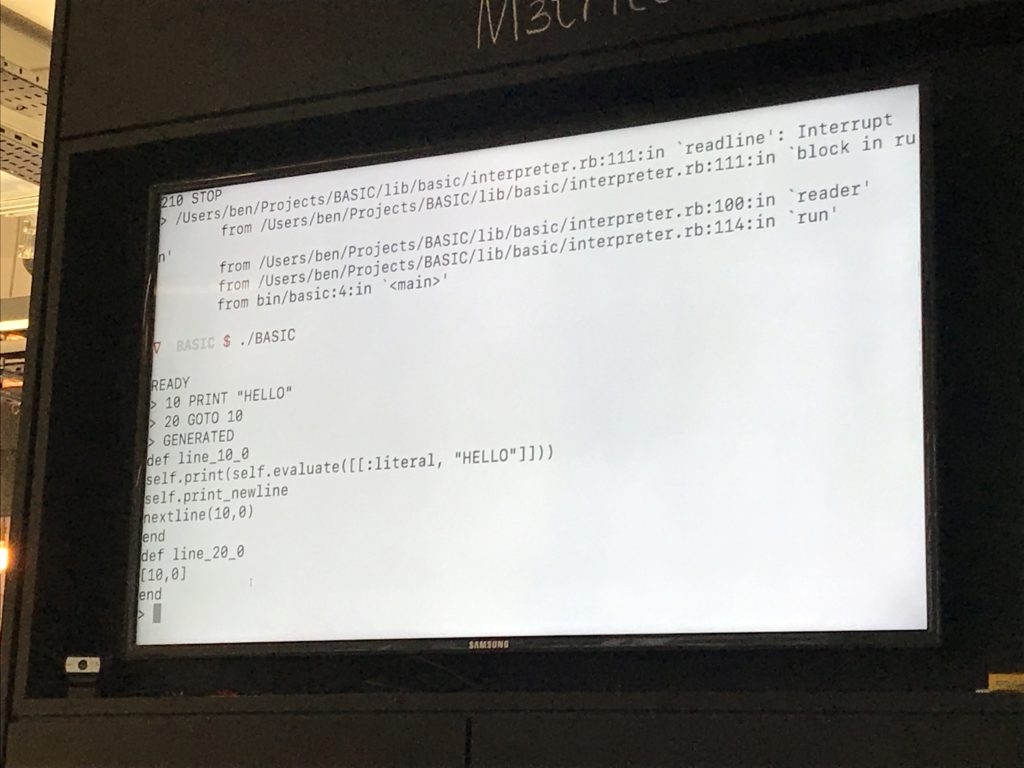
This was great, but Monsters of Galacticon was super tricky, a specific line preventing the eval strategy from working, and stopped work for 6 years.
So eventually Ben wrote a proper expression parser, and this used the shunting-yard algo to turn BASIC expressions into an RPN form that could be evaluated with a stack-based VM.
[aside: Leo: why are the line numbers multiples of 10? well, if you realise you need to insert a line between 10 and 20, you can define a new line 15 without renumbering everything (then use RENUMBER to print a rebased listing)]
Infix notation leads to ambiguities about evaluation order e.g.
10 + 2 * 3 => (10 + 2) * 3 or 10 + (2 * 3) ?
Operator precedence is a convention to standardise this without parentheses, so in the above example because * conventionally has a higher precedence than +, the second interpretation is used.
RPN / postfix notation lets you express these unambiguously (assuming you know the operator arity):
10 + 2 * 3 => 10 2 3 * +
Tom: you can think of RPN expressions as being a kind of program for a limited stack-based VM, where there are only two instructions:
- push a value onto the stack
- pop values off, perform an operation, push answer
Matt: how does this vary from lisp-style prefix notation?
Tom: this allows step-by-step evaluation, with a program counter moving along the expression token by token (stack-based vm vs register-based).
Okay, so how do we get from infix expressions to these postfix ones?
We discussed two variants of the algorithm - the basic one, where there is a single level of precedence, and the more complex one with multiple precedence levels.
Tuzz LEAPT to the whiteboard and wrote this example for the basic algo:
L O L O L O L
2 + 3 - 4 + 5
L = literal
O = operator
We were asked to believe that this key was accidental, but the reader can judge for themselves.
The basic case of the algorithm is simply:
* for each input token
* if it's an operator, push it to the stack
* if it's a literal, push it to the output, and push the whole stack to the output afterwards
This doesn't model precedence at all (or, I think, assumes all ops are of equal precedence).
The basic case having been ruthlessly dispatched, we moved on to dealing with precedence:
L O L O L O L
2 + 3 * 4 + 5
Precedence:
* = 2
+ = 1
- = 1
Now the algorithm is more complex - literals are still pushed to the output directly, but whether the stack is cleared depends on the next operator encountered. We only considered left-associative operators: when an operator is encountered in the input queue, we clear operators from the stack while they have a greater precedence than the new token.
We worked through this on the board. Choo-choo noises were made.
Associativity (I think) implies a kind of precedence among equal precedence operators
e.g. 1 + 2 + 3 => (1 + 2) + 3 because + is left-associative
whereas 1 ^ 2 ^ 3 => 1 ^ (2 ^ 3) because ^ is (conventionally) right-associative
This slightly modifies the precedence check when an operator is next in the input queue.
[HERE WE DECIDE TO SKIP BRACKETS AND FUNCTIONS AND MOB AN IMPLEMENTATION]
[GREAT AMOUNT OF PAUL DOING VIM STUFF CENSORED]
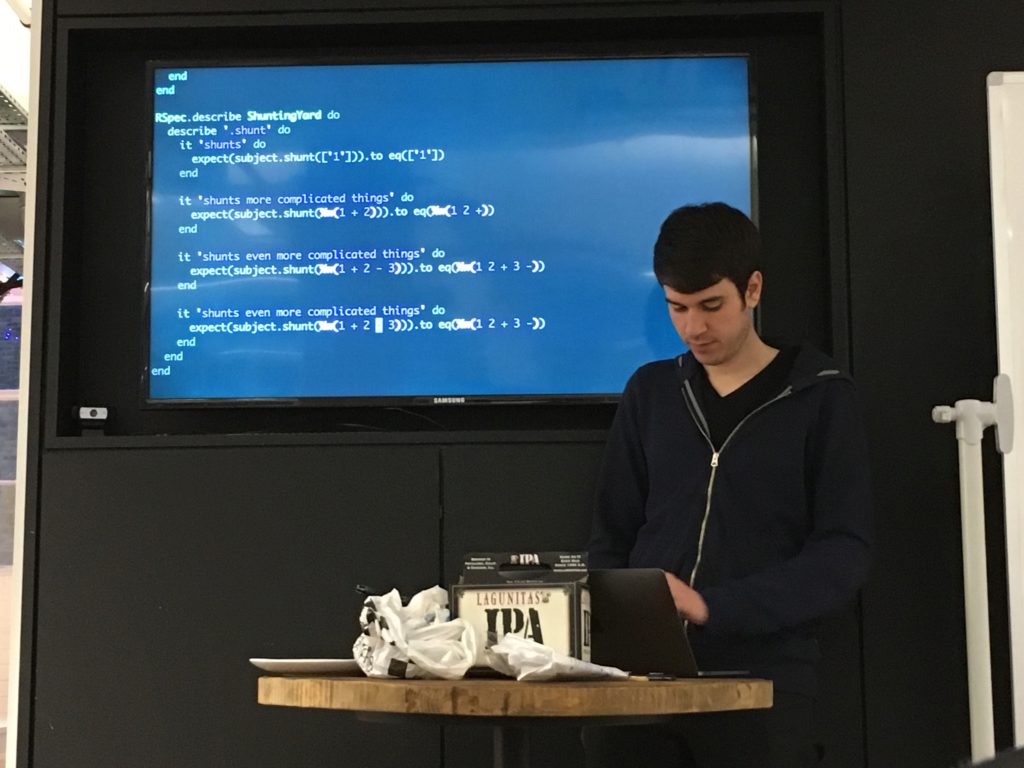
Some discussion of our model ensued. After a false start we agreed to have an object that could carry some state (our stack and output queue).
[INTERLUDE FOR TRAIN TERMINOLOGY DISCUSSION]
After some train-related pedantry (the best kind of pedantry), we decided that the stack was in fact a siding, and the whole object was the yard. This was approved. We ended the metaphor when Paul tried to call tokens "cars".
We quickly got to the basic implementation and started on precedence.
[NOISES OF JOEL PLAYING WITH WOODEN TRAINS BROUGHT BY BEN]
[MORE VIM NONSENSE CENSORED]
Chris Z CONTROVERSIALLY converted us from "siding" to "operator_stack", which, while unpopular, was an eminently sensible suggestion. Some discussion ensued about whether it really is a purely "operator" stack (since parentheses get placed on it, and they're not really operators), but we decided it was basically fine.
[TOM LIVESTREAMS HIS OWN FEET FOR SEVERAL SECONDS]
Okay, so we've got our stuff to the point where basic precedence works (no associativity), we decide to do parentheses next to override precedence in local circumstances
Ben: it's basically like you're creating a new stack - whatever happens inside the parens, the whole output of the inner expression should end up in the output, and then it continues as if nothing had ever happened.
Leo: what if we just create a new stack and recurse on the inner expression?
We talked this through and thought that, though it makes loads of sense, this might be a lot of complexity - we either need to decide how much of the input to pass down to the recursive call, or have some mechanism for passing the remainder up from the recursive calls.
Reader, we implemented it using the stack-based approach.
Tuzz: Can we hack the precedence system to implement brackets without a special parsing case? e.g. '(' has super high prec, ')' super low.
Tom: well, they're kinda special cased anyway in that they disappear in the final output, so maybe we don't gain any simplicity that way anyway.
Tuzz: could we move the special casing into an output filter that just rejects all paren tokens?
All: MAYBE WE COULD
Mudge: [SOUNDS OF TYPING]
All: OMG THAT ACTUALLY WORKED
Simon: but we've effectively set ')' to minus infinity prec, doesn't this mean that when we encounter ')', we clear the ENTIRE opstack instead of just up until the first '('?
Mudge: [SOUNDS OF TYPING]
All: YES IT DOES
Tom: I WANT TO PLAY WITH TRAINS
All: [MURMURED APPROVAL]
(You can find our final code in our shunting-yard repository.)
Mudge: This meeting, then. How was it eh?
Joel: purpose of this was to feel less like it's a long book haul, let more people in. Was this good?
All: [general murmurs of assent. maybe we haven't had loads of extra attendees but it felt refreshing innit. Takes pressure off the regular TAPL leaders.]
<3 <3 <3 <3 <3 <3 <3
Organisation: next time we agreed we should:
- pick an organiser
- organise it more than 7-10 days in advance so if there's an obvious person who's sharing a thing, they can prep
ACTION: identify the next natural break, it might not be part 2 of the book
Mudge: next tues Gecko can't host and it's right after Easter. Do we push the meeting back, push it forward?
All: not forward eh
Mudge: TO THE BAT-DOODLE!
All: nods of assent
Mudge: AN ORGANISER THEN?
All: [UNCOMFORTABLE SILENCE]
Abeer: I WILL DO THIS THING
All: [TUMULTUOUS ACCLAIM]