Cryptography, Padding Oracles

Notes

• A brief history of cryptography
  • Herodotus wrote of secret messages written on wood and covered in wax so that they appeared blank and, more outlandishly, writing a message on someone's head and waiting for their hair to regrow, swallowing balls of silk sealed in wax, invisible ink, etc.
  • Known as Steganography (steganos = covered, graphein = to write)
  • Works quite well but has a fundamental weakness: if the message is discovered, all information is revealed
  • So the development of Cryptography (kryptos = hidden), the message is not hidden but its meaning is so it can be intercepted but the information not lost
  • Transposition: where the letters retain their identity but change position, e.g. using a device such as a scytale
    • 
  • Substitution: where the letters retain their position but change their identity, e.g. the Caesar cipher
  • To simplify sharing algorithms (e.g. a substitution alphabet), can introduce the idea of a key which helps generate the substitution, e.g. a key word/phrase for the Caesar cipher
  • Symmetric-key encryption (share the same key)
    • 
  • Attack on substitution cipher if we know the language of the plain text: frequency analysis both of letters and pairs of letters (digrams), trigrams, etc.
• One-Time Pad
  • 
  • XOR message with key of the same length (XOR is addition modulo 2)
    • 
  • Preserves the randomness completely
  • c = m ^ k
  • m = c ^ k
  • Shannon's "Perfect secrecy"
  • Impractical in practice due to key length
• Block ciphers
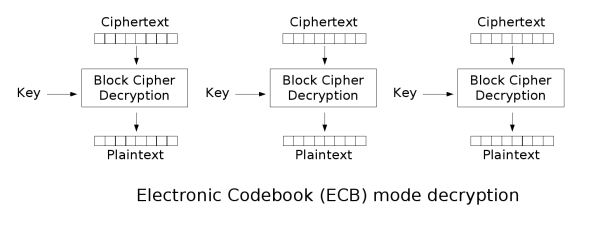
  • Electronic Codebook
    • 
    • 
    • 
  • Padding and PKCS7
  • The problem with ECB: the same message produces the same ciphertext
  • Cipher Block Chaining
    • 
    • 
• The Padding Oracle Attack
  • 
  • 
  • 
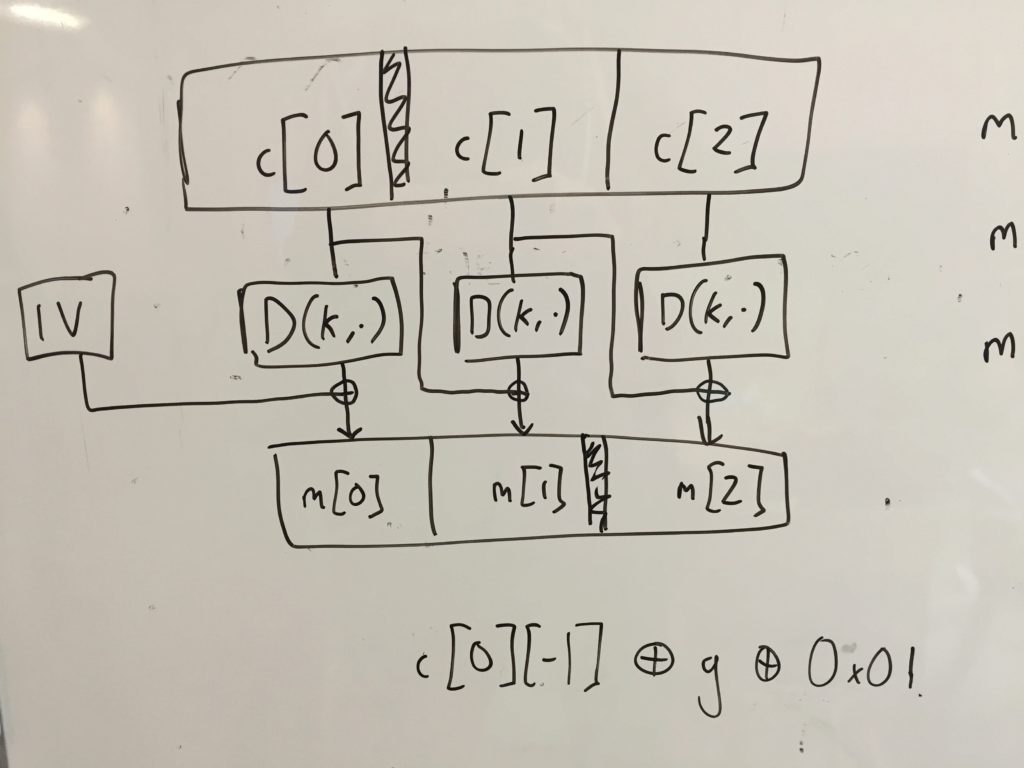
  • Review CBC and how encryption and decryption works, concentrating on XOR
  • Padding errors
  • Guess the last byte of a block by exploiting padding checks
  • What if there's no explicit padding error? Side-channel attacks still a possibility
  • Real world examples of vulnerabilities

References

• Simon Singh, "The Code Book"
• Dan Boneh, Stanford University, "Cryptography I"
• Rob Heaton, "The Padding Oracle Attack - why crypto is terrifying"
• Bruce Barnett, "CBC Padding Oracle Attacks Simplified – Key concepts and pitfalls"

Ruby Implementation

• An implementation of the padding oracle attack capable of decrypting a ciphertext encoded with DES and AES with cipher block chaining in Ruby: padding-oracles
  • 
  •