Skip to content

Parser Combinators

Jump to bottom Edit New page
Paul Mucur edited this page Jul 12, 2017 · 16 revisions

Introduction to Parser Combinators

We began the meeting by welcoming attendees new and old and James kicked things off by recapping his introduction to parser combinators.

The idea behind parser combinators is that each common operation in a parser can be implemented by a function, and then those functions can be combined into more elaborate operations. In general, a combinator is a function that takes an input state, typically the text to be parsed and an offset representing how far into the string you’ve already scanned. If the combinator matches the input at the current offset, it returns a parse tree and a new state: the text with the offset moved to the end of the text matched by the combinator. If it fails, it returns nothing, or the state it was given, depending on what’s most convenient for your implementation.

After explaining the core concept of parser combinators (covered more thoroughly in the aforementioned blog post) and touching on the issue of precedence and associativity in recursive descent, James introduced six useful combinators that he'd already implemented ahead of the meeting for us to mob with:

  • str(string, &action): match a literal string string and perform some action with the resulting tree;
  • chr(pattern, &action): match some character class pattern (e.g. a-z) and perform some action with the resulting tree;
  • seq(*parsers, *action): match a contiguous sequence of other combinators parsers and perform some action with the resulting tree;
  • rep(parser, n, *action): match another combinator parser at least n times and perform some action with the resulting tree;
  • alt(*parsers, &action): attempt to match the given combinators parsers in order and perform some action on the first matching combinator;
  • ref(name): an indirect reference to a named combinator, allowing us to form recursive matches.

Mobbing Time

With the core concepts in place, we decided to mob a parser for the arith language introduced in the early chapters of "Types and Programming Languages". Specifically, this minimal language:

t = true
    false
    t
    succ t
    pred t
    iszero t
    if t then t else t

Our first goal being to parse the following expression:

if iszero pred succ 0 then true else false

Into our own representation using Ruby classes like so:

If.new(IsZero.new(Pred.new(Succ.new(Zero))), True, False)

We began by implementing the "constants" of our language, 0, true and false by writing some RSpec tests and choosing some representation of our terms as plain Ruby objects.

Using James' existing ParserCombinators library as a starting point, we wrote our own Parser class with the following minimal rules:

class Parser
  include ParserCombinators

  def root
    alt(zero, tru, fals)
  end

  def zero
    str('0') { Zero }
  end

  def tru
    str('true') { True }
  end

  def fals
    str('false') { False }
  end
end

We then went on to add support for a slightly more complicated term: succ t which can contain any other term as its argument. We began with a failing test, detailing our desired outcome:

Succ.new(Zero)

And then added the rules to parse it:

class Parser
  def root
    alt(zero, tru, fals, succ)
  end

  def succ
    seq(str('succ '), ref(:root)) { |node| Succ.new(node.last) }
  end
end

As the node yielded to us for the term succ 0 would be the following Ruby array:

[:seq, [:str, 'succ '], Zero]

We simply take the last element of this array as the inner term we want to wrap in a Succ.

We then decided to relax the whitespace requirement so that we could also parse expressions such as succ 0 by extracting a separate whitespace rule:

class Parser
  def succ
    seq(str('succ'), whitespace, ref(:root)) { |node| Succ.new(node.last) }
  end

  def whitespace
    rep(str(' '), 1)
  end
end

We initially ignored Chris' pleas to abbreviate this to ws but later succumbed to defining an alias for whitespace called _.

With the liberal application of copy-paste technology, we had similar support for pred and iszero and then decided to do a Computation Club first: a little refactoring.

Specifically, we decided to introduce a brand new combinator just for this function call-like terms:

class Parser
  def function_call(name, klass)
    seq(str(name), whitespace, ref(:root)) { |node| klass.new(node.last) }
  end
end

This meant we could express succ, pred and iszero more succinctly:

class Parser
  def succ
    function_call('succ', Succ)
  end

  def pred
    function_call('pred', Pred)
  end

  def iszero
    function_call('iszero', IsZero)
  end
end

We were happy to discover that this meant we could parse arbitrarily nested terms like the following:

succ succ succ succ 0

Emboldened, we jumped into parsing our original goal by adding support for if t then t else t:

class Parser
  def root
    alt(zero, tru, fals, succ, pred, iszero, iff)
  end

  def iff
    seq(str('if'), _, ref(:root), _, str('then'), _, ref(:root), _, str('else'), _, ref(:root)) { |node|
      If.new(node[3], node[7], node[11])
    }
  end
end

The main trick here was trying to figure out the correct indexes into node which we double-checked by inspecting the raw AST output from our combinator:

[:seq,
 [:str, "if"],
 [:rep, [:str, " "]],
 "(iszero (pred (succ 0)))",
 [:rep, [:str, " "]],
 [:str, "then"],
 [:rep, [:str, " "]],
 true,
 [:rep, [:str, " "]],
 [:str, "else"],
 [:rep, [:str, " "]],
 false]

Having met our original goal, we were keen to get into thorny issues of associativity and so decided to spend the remaining time trying to implement the untyped Lambda Calculus, specifically the following Lambda expressions:

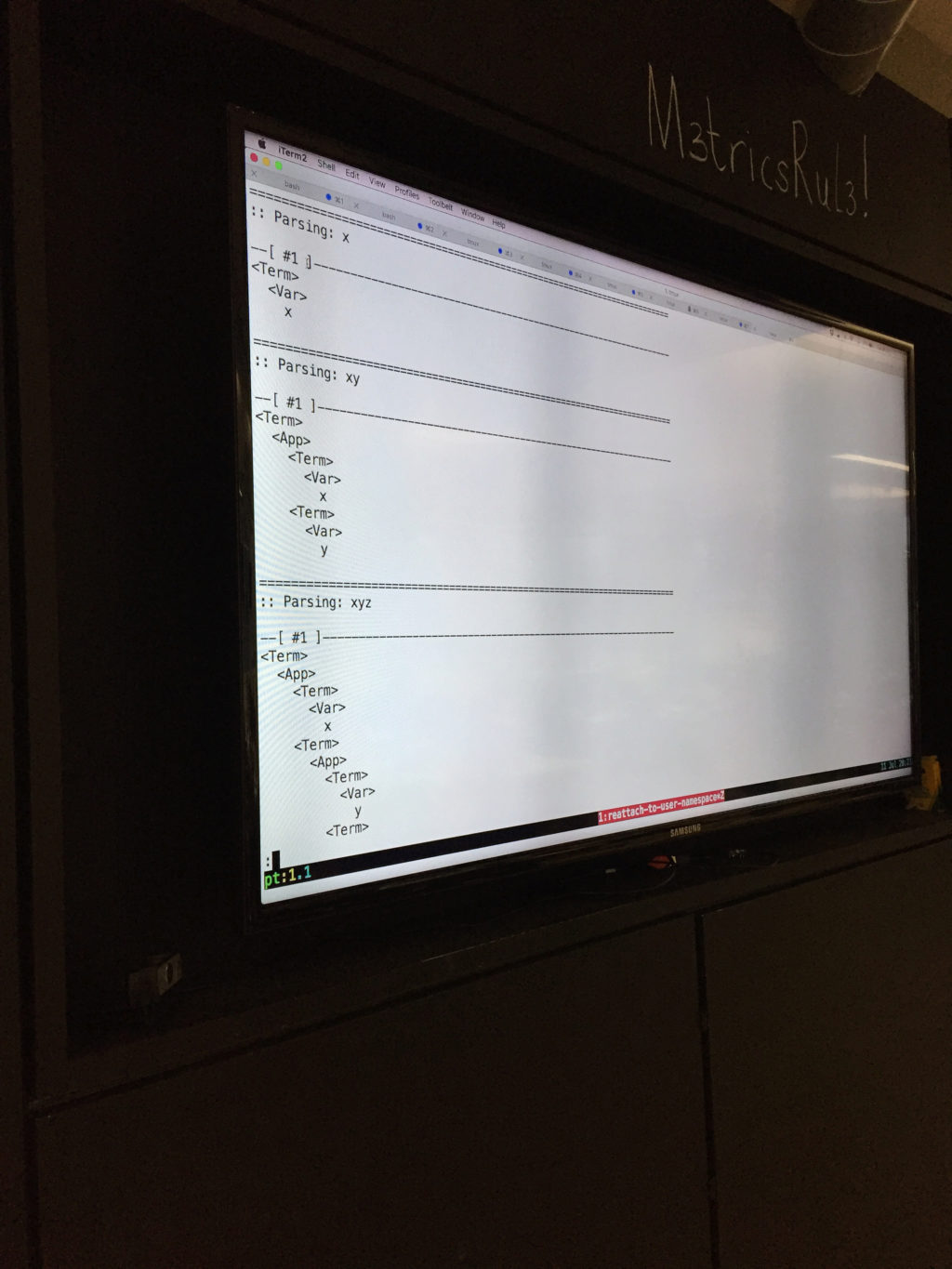
x
λx.x
λx.λy.x
x y
x y z

We began simply enough with variables such as x by defining them as a single lowercase letter:

class Parser
  def root
    alt(zero, tru, fals, succ, pred, iszero, iff, var)
  end

  def var
    chr('a-z') { |node| Var.new(node.last) }
  end
end

We then tackled abstractions:

class Parser
  def root
    alt(zero, tru, fals, succ, pred, iszero, iff, var, abs)
  end

  def abs
    seq(str('λ'), ref(:var), str('.'), ref(:root)) { |node| Abs.new(node[2], node[4]) }
  end
end

However, things started to get tricky when we approached applications. Our first test case of x y seemed straightforward enough:

class Parser
  def root
    alt(zero, tru, fals, succ, pred, iszero, iff, var, abs, app)
  end

  def app
    seq(ref(:root), _, ref(:root)) { |node| App.new(node[1], node[3]) }
  end
end

But disaster! Instead of a lovely App object, we got a dastardly nil. This was our first exposure to the importance of the order of combinators in an alt as we were attempting to parse x y as a variable first. This happily matched the x but left the rest of the input unparsed causing our parser to bail out and return nil.

Refusing to be defeated, we realised that we needed to re-order our combinators so that app (the "greedier" combinator) needed to precede var:

class Parser
  def root
    alt(zero, tru, fals, succ, pred, iszero, iff, app, var, abs)
  end
end

But oh no: it all went horribly wrong again and James cackled evilly to himself as we saw that this was an example of pesky left-associativity which is particularly tricky using this parsing technique.

More specifically, we were now attempting to parse x y by first calling root which then called app which then called root which then called app which then called... ad infinitum, never consuming any of the input and leaving us in a loop forever.

We decided to cheat a bit here and make our combinator a bit stricter instead:

class Parser
  def app
    seq(ref(:var), _, ref(:var)) { |node| App.new(node[1], node[3]) }
  end
end

This worked for our first case of x y!

Rapidly running out of time, we decided to tackle x y z which should be parsed as if it were (x y) z and not x (y z).

We decided to try something bold and parse the term in a right-associative way (as that is easy enough to do with combinators) and attempt to rotate the tree ourselves:

class Parser
  def app
    seq(ref(:var), _, alt(ref(:app), ref(:var))) do |node|
      case node[3]
      when App
        App.new(App.new(node[1], node[3].left), node[3].right)
      when Var
        App.new(node[1], node[3])
      end
    end
  end
end

This actually worked for x y z but sadly not for the more general x y z a. We thought of ways we might be able to resolve this with a recursive tree rotation but alas we were out of time.

You can find our finished code in our parser-combinators repository.

Show & Tell

James took a minute after the mobbing to show his work to implement a parser generating technique known as Unger's Method.

Paul briefly showed off his LALRPOP grammar in Rust for the fullsimple language from TAPL to contrast how left-associativity is handled by a bottom-up parsing technique.

Retrospective

  • Feelings were largely positive about the meeting and there was a lot of appreciation for the obviously large amount of work James had done to prepare for the meeting;
  • The specific focus of the meeting was praised as parsing is a very large topic (particularly compared to our previous interstitial).

Thanks

Thanks to Charlie for organising the meeting, to Geckoboard and Leo for hosting and providing beverages, to James for the huge amount of preparation and leading the meeting and to Laura for volunteering the organise the next meeting.

Add a custom footer
Clone this wiki locally