-
Notifications
You must be signed in to change notification settings - Fork 44
FAQ
CBC Casper is a family of consensus protocols, as well as a technique for defining new consensus protocols. All protocols in the family promise a variety of benefits over traditional consensus protocols, including:
- A simple (and shared!) consensus safety proof!
- Large flexibility to design consensus protocols on new data structures.
- The absence of an in-protocol finality threshold.
- Theoretically optimal message overhead, in certain cases.
This FAQ will give an overview of consensus protocols, introduce CBC Casper, and explore the above benefits and corresponding tradeoffs.
Imagine you're the owner of ten computers, and you want them to all agree on a random number between one and ten. However, these computers aren't always reliable, so you want to make sure that if some act unexpectedly (or totally crash) the remaining computers will still be able to agree on a value. How can you make sure that all correctly functioning computers will be able to agree on a number?
This is the problem of consensus. More formally, consensus protocols are processes by which nodes in a distributed network come to agreement. To be considered usefully, consensus protocols must satisfy a few properties.
The first property a consensus protocol must satisfy we call "safety." Simply put, it should be impossible for different nodes to make conflicting decisions. In our above example, if one computer outputs a three and another outputs a four, clearly nodes have not agreed on a value at all!
The second property is known as "liveness." Generally speaking, this means that nodes running the consensus protocol will eventually make decisions. To see why this is necessary, consider what would happen in our example if nodes never output a value. As no node would make a decisions, this protocol would clearly be satisfying safety (as no decisions means no conflicting decisions), but again nodes haven't agreed on a value!
At a first glance, coming up with a protocol that satisfies the properties of safety and liveness mentioned above seems fairly straight forward. For example, why not just have all nodes in the consensus protocol vote on a value, and then decide on the value that has the most votes?
The difficulty comes from two places. First, remember that these nodes exist in a distributed network. As such, we can't be sure that nodes see messages in the same order, or even see the same messages at all. Furthermore, some nodes send nonsensical messages, or multiple messages, or no messages at all.
Consensus protocols are hard because they must satisfy both safety and liveness even when some of the above problems occur.
In most standard presentations of consensus, nodes must agree on a bit: either a zero or one. In our toy example, we had nodes coming to consensus on a number between one a ten. However, consensus can be reached on a while wide world of other interesting pieces of data.
For example, we could have nodes come to agreement on an ordered list of financial (or other) transactions, or even a list of blocks!
As you will see throughout this FAQ, CBC Casper gives protocol designers a tremendous amount of flexibility to decide this exact question. We can create protocols in the CBC Casper family that come to consensus on all the above (and much more) with very little work!
CBC Casper research began as an exploration into Proof of Stake consensus protocols for public blockchains, but has since evolved into a more general branch of research.
There are currently multiple consensus protocols within the CBC Casper family, where different protocols come to consensus on different data types. Furthermore, CBC Casper research has expanded to include research into blockchain scalability in the form of sharding. We'll explore this more later in the FAQ!
Proof of Stake (PoS) is a proposed replacement for Proof of Work, which is the consensus algorithm that most public blockchains (Bitcoin, Ethereum) use today. If you haven't already, check out the Proof of Stake FAQ, which will hopefully convince you of the relative benefits of PoS. We will expand on these benefits throughout the rest of this FAQ.
CBC Casper can be classifies as one of the two main branches of Ethereum research. The other branch of research is known as Serenity, Ethereum 2.0, or Shasper.
Both branches of research are currently specifying Proof of Stake consensus protocols well suited for public blockchains. While these consensus protocols have a few major differences, much of the design criteria is shared. Furthermore, both branches of research are actively specifying scalability improvements for blockchains in the form of (sharding)[https://github.com/ethereum/wiki/wiki/Sharding-FAQ]. With these shared design goals, there's a large amount of collaboration between these two branches of research!
However, there are some major differences. Generally, CBC Casper research is more radical, less implementation focused, and farther from production. As such, Ethereum 2.0 will likely be the first improvement made to the public Ethereum blockchain. We look forward to seeing how these branches of research continue to inform eachother in the future.
For a more thorough overview of the history and current state of Ethereum research, check out this great overview here.
If you're coming from the current public blockchain world, the idea of a final decision in a consensus algorithm may seem foreign. After all, nodes in Proof of Work never make final decisions on a block. If a longer chain shows up at any time, a node will happily orphan any number of blocks in the shorter chain.
In traditional consensus protocols, and in all CBC Casper consensus protocols, this is not the case. Nodes are given the ability to make final decisions on values. In the blockchain world, this means the consensus protocol will lead to nodes making final decisions on blocks and never reverting them. We note that the safety of the consensus protocols implies that nodes will not make decisions on blocks that conflict - two nodes cannot decide on blocks that are on conflicting forks!
No. CBC Casper consensus protocols give nodes the ability to make decisions on blocks (or other values, depending on the consensus protocol) just based on the messages they've seen from other nodes. No developer checkpoints are necessary.
There are five parameters that go into the creation of a CBC Casper consensus protocol: the validator set, the validator weight map, the fault tolerance threshold, the consensus values, and the estimator. We will explore each of these parameters.
The validator can be thought of as the names of the nodes that are responsible for coming to consensus. In practice, this set can be the set of public keys of nodes participating in the consensus algorithm.
The validator weight map is a function that takes any validator and returns their "weight" in the consensus protocol. In standard consensus protocols, we think of all nodes being weighted the same; essentially, each node has a single "vote" in the consensus algorithm. For generality, CBC Casper allows different nodes to have different amounts of weight in the consensus algorithm.
This is also in preparation for Proof of Stake, where nodes will be weighted according to how much they have staked.
The fault tolerance threshold is, unsurprisingly, the parameter that represents the amount of faults that the protocol can tolerate. As this is a parameter, you might be asking "why not make it as high as possible?"
For one, this
How do estimates and decisions relate to the CBC Casper consensus safety proof? Also, what's a consensus safety proof?
A consensus safety proof, unsurprisingly, is what lets us call CBC Casper consensus protocols "safe." That is, it is a proof that protocol-following nodes will make the same correct decision (in some context).
There are two interesting aspects of the CBC Casper safety proof: first, it's very simple (compared to something like Paxos); second, this same proof is shared by every single protocol that is derived using the CBC Casper method. Here, we're going to work through the proof without any notation, but if you want a much-more-formal version, you can check out the Abstract CBC Casper Paper.
Here is a very rough outline of the safety proof:
- Every validator maintains a set of message they have seen. This is called a "view" or "protocol state."
- A validator can use an "estimator" to make an estimate about the current value of the consensus, based on their current protocol state (or set of estimates they've seen). For example, in binary consensus, the estimator would return a "0" or "1". In blockchain consensus, the estimator would say "the canonical blockchain is made up of block 0xaf42b...".
- Now, we define "estimate safety". An estimate is safe in a protocol state if it will be the estimate for any future protocol state. For example in binary consensus, if a validator can say "My estimate is 1, and no matter what messages I receive from other validators in the future, my estimate will be 1", then the estimate "1" is safe.
To complete the proof, we can show that making a decision on a safe estimate is consensus safe. That is, if validator 1 detects their estimate e1 is safe and validator 2 detects that their estimate e2 is safe, it must be that e1, e2 do not conflict with each other. For example, in binary consensus, it should be impossible for one validator to detect safety on "1" while another detects safety on "0."
To show that estimate safety leads to consensus safety is fairly straight forward. First, notice that we can construct a future-protocol state that both validators share by having each of them share all the messages they've seen with the other. By the definition of estimate safety, the estimate in the protocol state must be the same as both of their previous estimates. As one protocol state cannot have two conflicting estimates, thus these two validators must have not had conflicting estimates when they detected estimate safety!
In the above safety proof, we left out any mention of faulty nodes or validators. However, nodes crashing or acting in unexpected ways may may make make it impossible for other nodes to make a decision at the end of the protocols execution, or lead to different nodes making conflicting decisions. As we are interested in creating a fault tolerant algorithm, we have to make sure that our safety proof can handle these faults.
First, let us define the three main types of faults we have to worry about in CBC: crash faults, invalid messages, and equivocation.
Crash faults are fairly self explanatory and occur when a node stops making messages. We don't have to worry about these faults in our safety proof, because although crashed nodes may make it impossible for other nodes to make decisions, they can clearly not cause different nodes to make different decisions.
Nodes generating invalid messages is also a fairly easy, but broad, class of faults to understand. For example, if we are running a CBC Casper binary consensus protocol (where nodes are coming to consensus on either a 0 or 1), if a node makes a message the estimate 2, this is clearly invalid. There are other types of invalid messages that are more interesting than the above example that we will expand on later in the FAQ.
Equivocation is probably the most interesting of the possible faults. Essentially, a node is equivocating if it's running two copies of the consensus protocol that are unaware of each other, at the same time. For example, if a validator simultaneously makes two messages, one with an estimate of 0 and another the estimate 1 (where neither message acknowledges the existence of the other message), we say this validator is equivocating. Clearly, this type of behavior is bad when we are trying to get nodes to come to agreement on a value.
Now that we are equipped with knowledge about what faulty validators actually look like, we can talk about we handle them in the safety proof.
Recall in the last step of the safety proof, when we said that two validators who both detected estimate safety had the same estimate, as we knew they shared a common future protocol state that must have this estimate as well (by the definition of estimate safety).
Thus, to handle faults in the safety proof, we simply add a condition that some set of messages ceases to be a valid protocol state if it contains greater than some number of invalid messages or equivocations. Thus, nodes are assured they will make the same decisions if the common future that they share contains less than some number of faults.
For more detail on the above, check out the Casper TFG specification.
In the above safety proof, we said that validators could make decisions on estimates that are safe. Thus, to complete the specification of our CBC Casper protocols, we must give validators a technique for detecting when their estimates are safe, so they can make decisions!
We do this by specifying a variety of "safety oracles" for validators to use. Safety oracles take as input a protocol state and some estimate, and return true if the estimate is safe in that protocol state and false otherwise. There are multiple oracles as some may be better suited for different situations (e.g. on resource-constrained devices).
Furthermore, some of the oracles described below can explicitly calculate the "minimum amount of safety" that an estimate has.
Currently, there are three safety oracles that exist in the proof of concept codebase.
Given a protocol state and some estimate, the adversary oracle creates models of all other validators in the network and simulates these validators conspiring to change this estimate.
If it can simulate some protocol execution that leads to this estimate changing, then the attack has succeed, and the oracle will return false, as the estimate is not safe. If it can find no future protocol state where the estimate is different, then the estimate is safe, and the oracle returns true.
Note that this adversary oracle is not an "ideal adversary," in the sense that it's attack may succeed where it would fail in the real world. This is a result of the adversary oracle being a lower-bound due to efficiency reasons.
Note that this oracle is a lower-bound in one direction: it will never say an estimate is safe when it is not safe, but it may say an estimate is not safe when it is safe. This technique of making the oracle a lower-bound is used in all current safety oracles, as it generally makes reasoning about the oracle easier and running them more efficient.
At a high level, the Clique Oracle can be thought of as looking at a given view and deciding if it is worth attacking with the above adversary in the first place.
First, from the protocol state and given estimate, we construct a graph in the following way:
- Create a node for each validator in the graph.
- For each pair of validators, if each validators has a latest message the other with the given estimate and cannot see a message from each other in the future that is not on the given estimate, create an edge between them.
The name of this oracle gives a good clue as to the next step: we search for the biggest clique of validators in the graph. If this clique is greater than 50% by weight, then we can say that we have some degree of fault tolerance on this estimate. Otherwise, the majority of validators are not locked into this estimate, and we cannot say this estimate is safe.
The intuition for this oracle is fairly straight forward: as the estimator functions are determined by validator weight, if the majority of validator weight is locked into seeing a single estimate, this estimate is safe.
Note that this oracle is also a lower bound and only recognizes safety in certain situations.
This oracle uses a very similar process to the Clique oracle, in that it considers edges between validators in graph. However, instead of performing a search for the largest clique in this graph (or even constructing the graph), the oracle uses Turan's Theorem to find the minimum size of a clique that must exist in this graph.
From there, it uses the same process as above to detect if the estimate is safe as well as calculate the (minimum amount of) safety that must exists on this estimate.
There are many other designs for oracles that may/will exist in the future that should be explored, exploring different points of the efficiency/lower-bound tradeoff curve.
Some criteria must be preserved across safety oracles; for example, if a safety oracle can recognizing an estimate is safe in some view, it should clearly be able to recognize these estimates are safe in future views.
If you're interested in thinking about safety oracles (and maybe designing/implementing some), you can join the conversation here.
Isn't it easy to recognize some trivial cases where an estimate is safety? For example, if all of the validators have the same estimate, can we safely decide on that estimate?
Surprisingly, no. It's worth talking about this because it's actually fairly unintuitive.
To detect safety, we need to be able to say more than just "validators latest messages have the same estimate," as there may be as-of-yet-undelivered messages floating around the network. This is a result of wanting to be able to have a consensus protocol that is safe with no timing assumptions!
Reasoning about the possible existence of these messages (and figuring out if there's any possibility they will change the validators' estimates) is exactly what the oracles described above do.
They do this by taking advantage of an as-of-yet-unmentioned part of every CBC Casper consensus protocol. That is, whenever a validator makes a message, they include with it a commitment to the other messages they've seen from other validators. This is called a "justification." With this, it becomes possible for us to reason about what undelivered messages might be floating around the network.
A consensus protocol that is safe with no timing assumptions is called an asynchronously safe consensus protocol. Asynchronous means we make no assumptions about how long it takes messages to deliver, while a synchrony assumption means we assume there is a maximum time it will take a message to be delivered.
All protocols derived using the CBC approach are asynchronously safe consensus protocols.
All CBC Casper consensus protocols are derived to satisfy the above consensus safety proof, and thus different protocol-following nodes will not make conflicting decisions in some context.
However, having a safe consensus protocol isn't enough for our protocol to be useful. For example, we can trivially create a safe consensus protocol by saying "no nodes are allowed to make decisions ever." It's clearly impossible for them to make conflicting decisions in this case.
We must further show that CBC Casper consensus protocols will be useful, in the sense that they will actually produce decisions on values. We'll simplify a bit and call this liveness.
// TODO: talk about plausible liveness??? can't get stuck???
There's still some work to do as far as specifying/measures/proofs of liveness.
For the purpose of this comparison, we will split all existing PoS consensus protocols into two groups: those with deposits and slashing and asynchronous safety, and everything else.
All Casper protocols (FFG, TFG) satisfy this condition, as well as other protocols such as Tendermint. Many other protocols (such as early-day PoS algorithms and current DPoS protocols) do not satisfy these conditions.
The arguments for deposits and slashing conditions are fairly straight forward: without these, we have to make significantly more assumptions about the coin-holders/validators for the protocols we make to be safe. As a side note, if you're unsure what slashing conditions are, see here.
Furthermore, having access to validator deposits give us significantly more control over the participants in the protocol...
The argument for asynchronous safety also follows the same logic: it's a much weaker assumption to make than "all messages will be delivered within some bound," and as such is better suited to the extremly adversarial public blockchain world. Making a timing assumption that's shorter than the order of, say, weeks, can be a danger for public blockchains.
Within the category of the protocols that have deposits, slashing, and asynchronous safety, further differences can be noted, of course. For a treatment of the subject, check out this Tendermint blog post.
Another way of classifying different fault tolerance consensus protocols is through the context of a "tradeoff triangle."
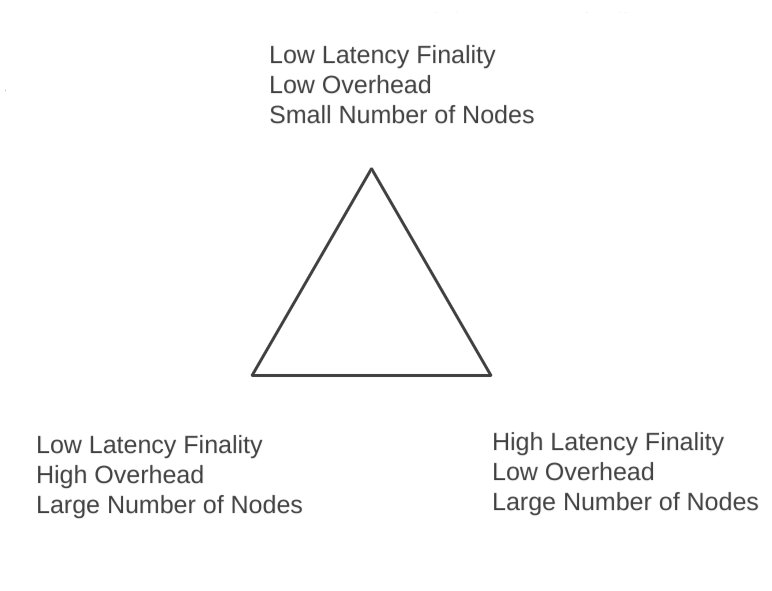
Essentially, all fault tolerance consensus protocols are forced to make tradeoffs, between the number of nodes that come to consensus, the communication overhead of the consensus protocol (on a per block or decision or second basis), and how long it takes for finality to be reached. To understand the triangle more fully, we can explore some consensus protocols on where they exist in within the triangle.
Consensus protocols that only create finalized blocks have low latency and parameterizations in the purple area in the picture below.
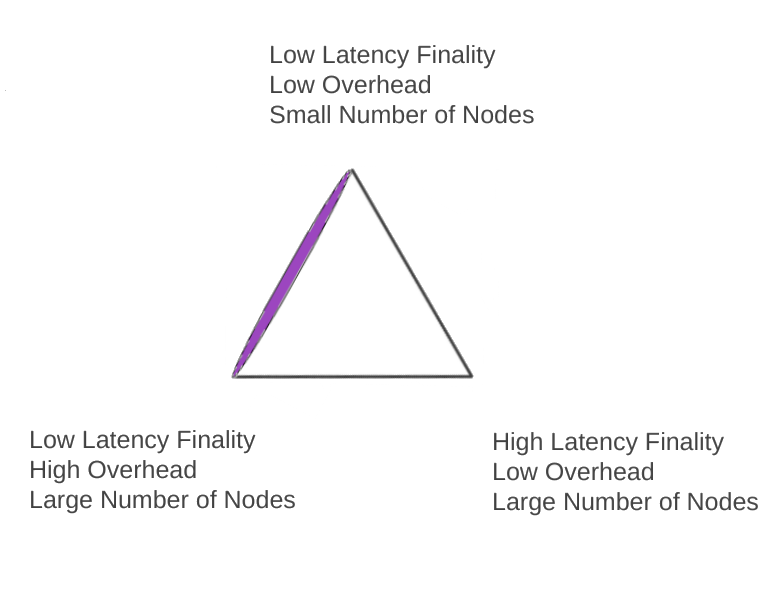
Note that their their overheads for any different node counts may vary. Some examples of these protocols include Tendermint, Honey Badger, Dfinity, and PBFT.
Traditional blockchain protocols, on the other hand, have no finality, but can have an arbitrarily high number of consensus-forming nodes with the same incredibly low protocol overhead. They exist in the purple dot on the below graphic (because they lack finality):
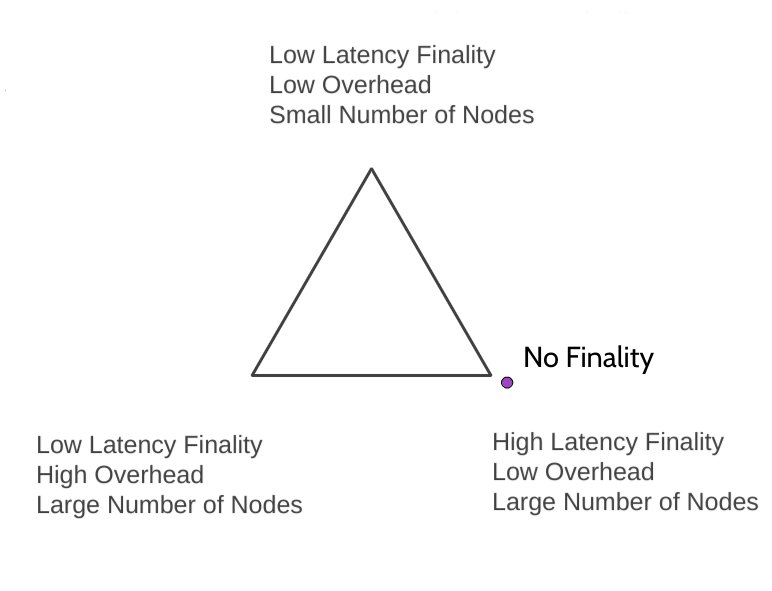
Examples of these protocols include Nakamoto Consensus, PPC, NXT, Snow White, Ouroboros and many other PoS protocols.
The question remains: where does CBC Casper exist in this triangle? It can't avoid making the tradeoff (no one can), but, perhaps it can exist with a parametrization in the middle of the tradeoff triangle with a reasonably low latency to finality, reasonably large number of validators, and reasonably low overhead.
Notably, in the case of maximally low overhead for any number of validators, the latency to finality is finite (though unbounded), unlike in Nakamoto consensus or most proof-of-stake protocols, which have no finality (or, if you like, infinite latency to finality).
To talk about Casper FFG, we should be clear about whether the overhead's basis is per underlying PoW block (in which case its parameterizations can explore the tradeoff fully), or per decision (in which case it's like PBFT and is stuck to one side of the triangle).
If you want more reading about the tradeoff triangle, see a great post from Vitalik on the issue here, or Vlad's original twitter thread here.
Traditional consensus protocols explicitly tolerate up to f faults, where f is some number of the n nodes that are coming to consensus. That is, if more than f nodes are faulty in some way, then the consensus protocols may cease to give any guarantees to nodes coming to decisions, and two nodes may decide on different outputs.
The safety proof of these protocols relies on each node tolerating at most f nodes failing. This is a in-protocol fault tolerance threshold, as the all nodes must have the same value for f.
You may hear this referred to by "____ can tolerate up to 1/3 of validators, by weight, being faulty." This assumption of at most 1/3 of validators being faulty is an in-protocol fault tolerance threshold.
CBC Casper is unique as it does not need an in-protocol fault tolerance threshold. That is, different nodes can decide different values for the amount of faults that they are willing to tolerate. TODO: reword.
We will explore the benefits of an out-of-protocol fault tolerance threshold in a later question.
Many protocols use 1/3 as the maximum number of faults they can tolerate, and it's reasonable to wonder why this is the value. Essentially, this number walks the line between tolerating safety and liveness faults.
For safety reasons, we don't want validators that are following the protocol to make different decisions. For liveness, want them to be able to make a decision.
Now, let's say we have n total nodes who are trying to reach consensus, of which there are f byzantine nodes. Finally, we say that at least t nodes must "agree" for there to be a decision.
First, let us consider safety. Let's say that the n - f nodes are split into two equally sized groups of (n - f) / 2. Because the f nodes may act arbitrarily and tell each equal sized group different things, we want to make sure that (n - f) / 2 + f nodes isn't enough to make a decision. If it is, the two equal sized groups could decide different things, and we would have a safety failure. Thus, we know t > (n - f) / 2 + f.
Now, let us consider liveness. We want to make sure that the n - f nodes can come to consensus, else the faulty f nodes going offline could stop the rest of the nodes from coming to consensus. Thus, we know n - f >= t.
We can combine the constraint n - f >= t and t > (n - f) / 2 + f, to that get n - f > (n - f) / 2 + f. With some basic algebra, we know n/3 > f. Thus, this is why 1/3 is used as the traditional fault tolerance threshold in many protocols.
We'll be brief here, but most consensus protocols we're discussing here (PBFT, Tendermint, Casper FFG) have a build in concept of "rounds" or "epochs." As such, they need the property that if some of the validators advance to the next round, all the validators need to advance with them, else the protocol can get stuck.
The argument can be generalized to: nodes with the same set of consensus-relevant messages much have the same "estimate" on what they think consensus is, otherwise they may get stuck. So far, all proposed round-based protocols do not have this property.
Because CBC Casper has no concepts of rounds, all derived CBC protocols have the property that no matter a nodes fault tolerance threshold, they will have the same estimate as nodes with the same set of consensus-relevant messages (assuming less than the number of faults in the common future of these nodes).
As such, it is possible for CBC Casper to remove the fault tolerance threshold from the protocol entirely; nodes can choose the amount of other nodes that they will tolerate equivocating.
Here, we will briefly venture into "mechanism design for Casper protocols", specifically in the context of PoS protocols for public blockchains.
Essentially, have an in-protocol defined fault tolerance threshold gives cartels an incentive to form around these points. For example, consider that if 2/3 of validators can finalize blocks with no input for the other validators, this creates two focal points for cartels to form: 1/3 + e, and 2/3 + e.
The smaller cartel can stop any blocks from being finalized, and the larger cartel can finalize blocks without any input from the other validators (not at the same time, of course). In the case of public blockchains, as cartelization and centralization concerns should be the forefront of our minds, this is clearly a dangerous concern. As such, being able to remove the fault tolerance threshold from the protocols is beneficial as makes it harder for cartels to form and perform the above attacks.
You can read more about the goals of making Casper cartel resistant in this History of Casper posts, 1(https://blog.ethereum.org/2016/12/06/history-casper-chapter-1/), 2, 3, 4, and 5
When talking about efficiency (specifically for Casper TFG), there are two major efficiency considerations: validator overhead and network overhead.
For validator overhead, there are two important considerations: the forkchoice, and safety detection. In both cases, there are some clever optimizations we can make to minimize the amount of work validators have to do.
The optimizations to the forkchoice are fairly straight forward. As the forkchoice follows the Greedy Heaviest Observed Subtree Rule, you can imagine we can take some graph G that represents the blocks and reduce it to some graph G', where G' is a graph with the minimal number of nodes that are needed for the forkchoice to run and return the same output.
For example, let's imagine we have blocks A, B, and C, where A <- B <- C (A is the parent of B, B is parent of C, A is the genesis). In this case, it's clear that determining the forkhoice is pretty easy: the intermediate node B isn't really needed - and so we could remove it in the reduced graph that the forkchoice runs on.
The safety oracle optimizations are described in the questions about safety oracles above. In general, safety oracles can be make more efficient by making them a lower bound as well as cacheing.
If you're interesting in specifying and/or implementing on either of the above optimizations, please reach out!
For network overhead, see the above section discussing the tradeoff triangle. TL;DR: Casper TFG has the ability to tradeoff time to finality, number of validators, and network overhead in any direction it wishes!
Sharding is a proposed method for scaling blockchains. You can read another great FAQ about it here. Sharding fits nicely into the CBC approach, as one of the data structures we can replicate is a sharded blockchain!
You can see the start of some research here. There's also a good talk on CBC Casper sharding, linked in the resource list below.
Check out the resource list! It contains all the resources for understanding CBC Casper that you could ever want :D