A program in Walking Robot course.
- the 'main.py' file is the entrance of the program, you can adjust the paramaters, like step period, step height, in this file
- the 'QuadrupedSim.py' is the core code for the program, primary simulation function and control function are all included in this file;
- the main function for 'Planner.py' is design a target trajectory for the toes, currently we use the compenont curve as the trajactory.
- the 'test.py' is original file for the program, 3 files above are base on this file
- ‘mini_cheetach2.urdf’ is downloaded from Google, which is xacro form, it's more convinient to modify paramaters for robot compared with the model in pybullet dirctory
- 'meshes' includes file used for modeling
- 'mpc_stance_controller' is the file including using the MPC controller of the stance.
- 'mpc_osqp' is the file designing the MPC controller of the stance and also includes osqp in C++.
Final Project 理论介绍
相比于传统的基于多刚体系统建立各运动关节的高频反馈控制的动力学模型
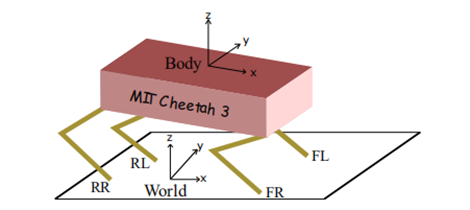
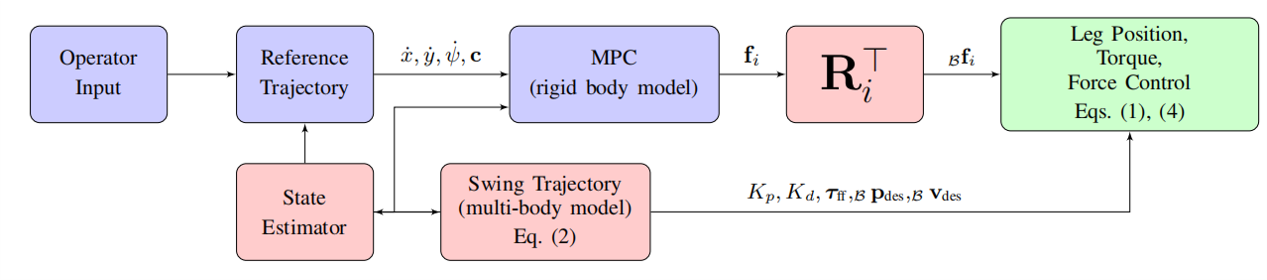
为了实现四足机器人运动和动力学模型的简化,我们将整个四足机器人看成一个单刚体模型,但是又保留它的动力学特征,这一点在下图控制系统的蓝色框中得到了体现,即在单刚体模型下进行MPC的控制,但是这并不会输出各关节的力矩,而是把控制问题分割成先求地面反力,再通过各个机械臂的力雅克比矩阵求得关节所需要的的力矩,其中,力雅克比矩阵可以通过电机位置姿态以及机械臂的力约束矩阵求得。MPC控制模块输出的地面反力是机体坐标系下的,需要对其进行坐标系转换,然后通过矩阵映射求得相应的电机扭矩,实现力控。
对于摆动相,则通过轨迹的设计和状态机的调整,基于PD控制和前馈控制实现位置控制
下面,着重介绍一下MPC控制模块在我们本次项目中所需要的理论(图片均为项目内PDF截图):
首先是描述机器人状态的主要变量的选取。对于机器人自身运动状态的描述,姿态以及位置层面,是使用欧拉角(roll ,pitch,yaw)和质心位置(x,y,z)来描述,同时为了描述其运动信息层面,加入角速度以及机器人质心的运动速度。因此,在机器人状态描述层面,共有姿态角、质心位置、姿态角角速度、质心速度共12个量描述
首先是关于质心加速度的牛顿公式
对于任何踩在地上的足式动物或者是足式机器人,他们所受到的外力无非是重力和地面反力,通过对该整体进行受力分析,我们得到了加速度,即位置的二阶导数的等式
对于欧拉角的旋转矩阵,我们可以通过z轴旋转yaw的角度,再通过当前坐标系的y轴旋转pitch的角度,再通过当前坐标系的x轴旋转roll的角度,从而得到欧拉角的 旋转矩阵,对于yaw来说,roll和pitch属于小量,他们进行近似,从而得到只有z轴旋转矩阵的表达关系,同时,对于欧拉角的角速度,我们可以通过将角速度进行xyz轴的分解,通过将轴上分解角速度进行坐标系上的变换即可得到欧拉角速度和角速度之间的关系。
下面是欧拉公式的近似转换和空间惯量的张量在坐标系下的变换,我们通过公式,建立了转动惯量与角速度的导数和地面反力产生的力矩的数学关系,并以此推导出角加速度,同时,在这个公式中,由于角速度作为小量是可以被忽略,并且如果角速度这一项被添加,可能会导致求解的发散
同时,我们还要将各个坐标系下的转动惯量转换为世界坐标系下的惯量。
接下来便是状态空间模型的搭建,我们将刚刚所讲的运动学和动力学公式进行整理,并将其离散化,就得到了Ak和Bk的矩阵。并且还有一点值得一提,为了后续的计算简便,我们将重力加速度也并入了状态量,使得状态量从12维变成15维,同时Ak也变成一个15*15的矩阵
并且这里的离散化在代码实现上也很有讲究,不同于原本的A+I*dt,我们选择将A进行指数化,即exp(A)
然后就是MPC的设计,我们目前已经将fk当做成一个输入量,所以说我们的设计目标就是通过一个合适的输入量,来达到一个可靠最优的轨迹跟踪的效果,这跟大家所熟悉的LQR控制非常的类似,事实上,相比于LQR系统,MPC控制也只是多了一个给定HORIZON的预测部分,通过不断的对AB矩阵的计算和迭代,我们得到一个全新的线性模型,我们可以将这个矩阵写作Aqp,另外一个矩阵写作Bqp
接下来的任务就是将该类MPC模型问题转换一个二次优化模型,通过最小化下方的代价函数,求得一个最优的输入值,也就是地面反力值,
这个公式着重于轨迹之间的差值,并附有Q和R这些权重矩阵。通过把x这些非输入项进行替换,我们就得到了右边这个标准二次型求解问题,其中H和R都可以用上述这些Aqp和Bqp矩阵来表示。然后我们可以通过C++库中的二次规划求解器解出我们期望的地面反力。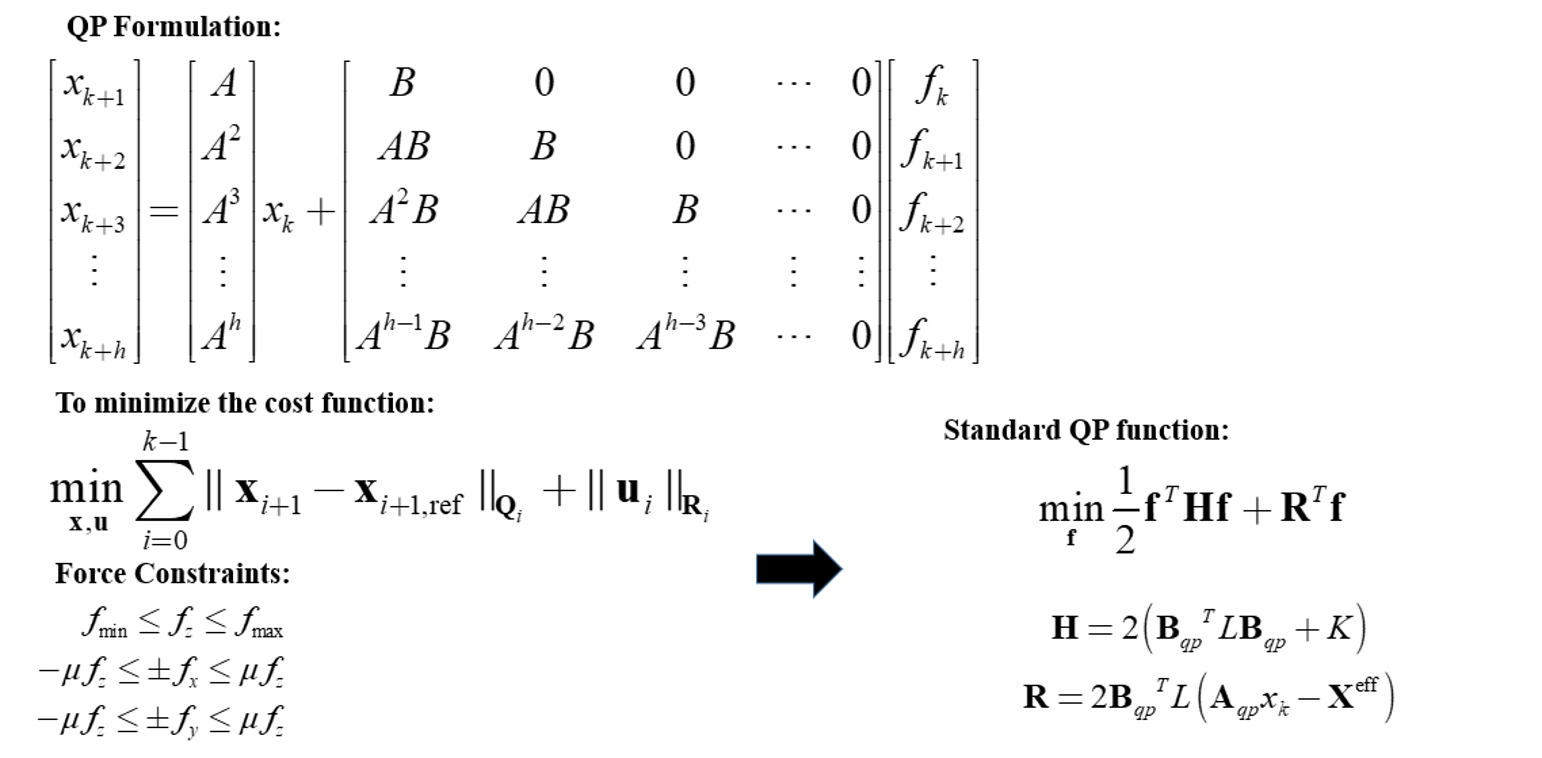
以下是GIF演示:
没有MPC,只有位置控制:
MPC第一代:
MPC第一代在崎岖路面(dH = random(0,0.05)):
MPC第二代:
MPC第二代在崎岖路面(dH = random(0,0.01)) 效果并不理想: