This repository contains a C++ implementation of some of the Graph Algorithms: Minimum spanning tree (Prim's Algorithm) & Shortest Path Finding (Dijkstra’s Algorithm).
This team (me and @oswidan97) work was developed as assignment for Data Structures & Algorithms Course Spring 2018 offering at CCE department, Faculty of Engineering, Alexandria University.
-
The main goal is to become familiar with the graph data structure, its algorithms and applications.
-
A Graph is a non-empty finite set V of elements called vertices together with a possibly empty set E of pairs of vertices called edges G(V,E).
-
A weighted graph is a graph, in which each edge has a weight (some real number).
-
Weight of a Graph is the sum of the weights of all edges.
-
A Minimum Spanning Tree in an undirected connected weighted graph is a spanning tree of minimum weight (among all spanning trees). The minimum spanning tree may not be unique. However, if the weights of all the edges are pairwise distinct, it is indeed unique.
-
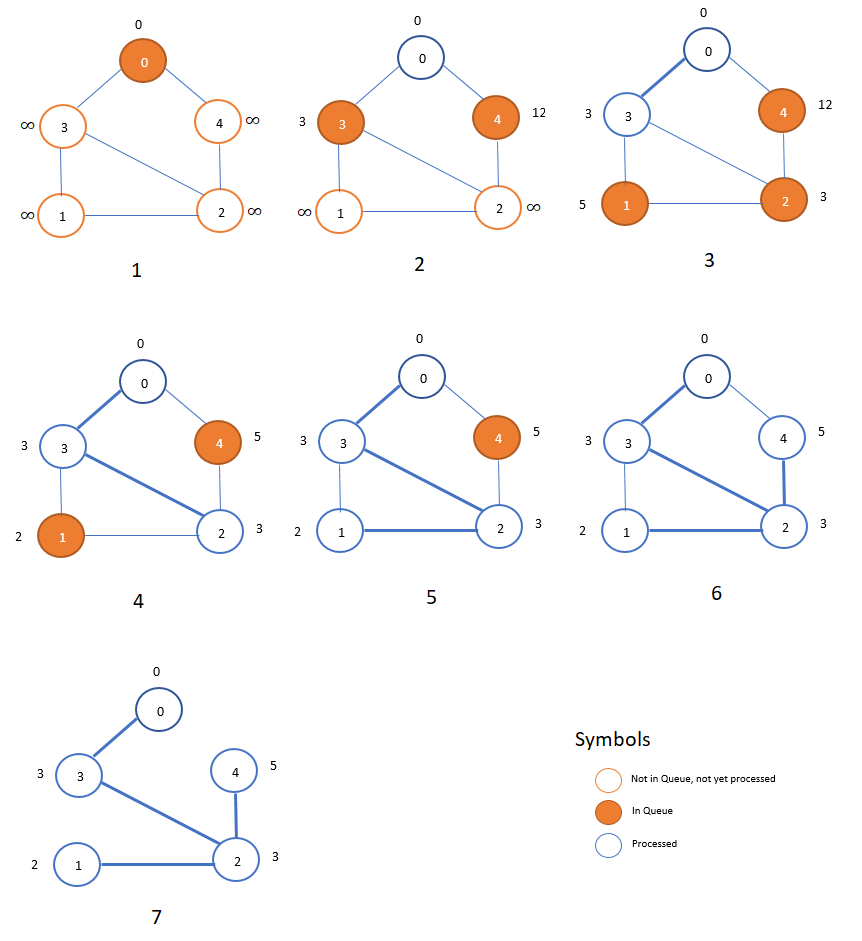
Solves the MST (MInimum Spanning Tree)Problem: Given a connected weighted undirected graph G , design an algorithm that outputs a minimum spanning tree (MST) of G.
-
The Prim’s algorithm makes a nature choice of the cut in each iteration – it grows a single tree and adds a light edge in each iteration.
-
Input: Weighted undirected graph, single source s.
-
Output: Edges (MST) using Prim’s algorithm starting from s to include all vertices.
-
Solves the Shortest Path Finding Problem: The shortest path between two vertices is a path with the shortest length (weight).
-
In particular, the Dijkstra’s algorithm is a solution to the single-source shortest path problem in graph theory, and solves for both directed and undirected graphs.
-
Constraints:
- All edges must have nonnegative weights.
- Graph must be connected.
-
Input: Weighted directed graph with positive edge weights, single source s.
-
Output: the distance of a shortest path from the source vertex to every other vertex in the directed graph using Dijkstra’s algorithm.
1. Minimum Spanning Tree (MST) using Prim’s Algorithm Tutorial, Used the figure.