Multiple Bases Compression Algorithm

An algorithm I came up with one night to combine and compress information with multiple bases. I do not know if this has been discovered before. The closest algorithm I can find is the Double Dabble algorithm. Mixed radix uses the same idea, but not for the same purpose.

Problem

Let's say you have 3 pieces of unrelated information. The first piece can be in one of 3 states. The other two have 4 and 5 states, respectively. A naive approach would store this information in 7 bits ($2+2+3$). However, the optimal number of bits to store this information is 6: $\lceil{\log_2(3\cdot4\cdot5)}\rceil=6$. This algorithm can store such information optimally.

Simple case

Let's store 3 pieces of information, each with 10 possible states, in the minimum 10 bits. The naive approach would use 12 bits. We can represent each piece of information as one base-10 digit. Therefore we'll end up with a 3-digit base-10 number, with a maximum value of 999, and 1000 possible states total. This can be converted to binary to be stored in 10 bits.

General case

We will now store 3 pieces of information, 3, 4, and 5 states respectively, as in the introduction. The naive approach uses 7 bits. We start with a number 0 that is our encoded information. We add to it the first piece of information (3 possible states, from 0 to 2). Next, we multiply the second piece of information (0 to 3) by the amount of possible states in the first piece (3). We add the product to the encoded number. For the final piece of information, we multiply it (0 to 4) by the amounts of possible states in the first two pieces ($3\cdot4$), and add it to the encoded number. The encoded number will have a minimum value of 0, and a maximum value of $2+3\cdot3+4\cdot4\cdot3=59$. Taking $\log_2(60)$ (60 possible states for 0-59) and rounding up, the encoded number requires 6 bits to store.
This can be expanded to use more pieces of information, and different amounts of states for each piece.

In short, the algorithm works by creating a number with each digit having a (potentially) different base (ie. base 2 for one digit, and base 10 for another).

Decoding

For decoding, we assume we already know how many pieces of information are encoded, how many states each piece can be in, and the correct order. We will use the example above. First we check the value of the piece of information with 5 different states. We take each of the possible states (4 to 0), and multiply them by ($4\cdot3$). We check each of them to see if they are less that the encoded number. If yes, then subtract it from the encoded number and divide by 12 to obtain the first piece of information. Repeat for all pieces of information.

Implementation

The example implementations are written in Python 3.
Encoder
Time complexity: O(N(A+B)), where:

• N is the amount of pieces of information
• O(A) is the time complexity for addition
• O(B) is the time complexity for multiplication

Decoder
Time complexity: O(NM(A+B)), where:

• N is the amount of pieces of information
• M is the average number of possible states for the pieces of information
• O(A) is the time complexity for addition
• O(B) is the time complexity for multiplication

Note: the speed of the decoder can be improved using modulus.

The reason the time complexities for addition and multiplication matter is because the numbers used can get very large.

Use cases

This algorithm probably has very few use cases, since most information is already stored in base-2 friendly values. However, there are two (obscure) cases I can give where this can be useful: Scratch cloud variables and Desmos. For Scratch, the information to be stored can be in the form of different bases, and the space to store it is very limited. This problem of maximizing information density is what inspired me to develop this algorithm. For desmos, this algorithm could provide a way to store a little extra information within the 5 MB graph size limit (yes, this matters for some projects).

Desmos Implementation

The user ronwnor created an implementation for desmos:

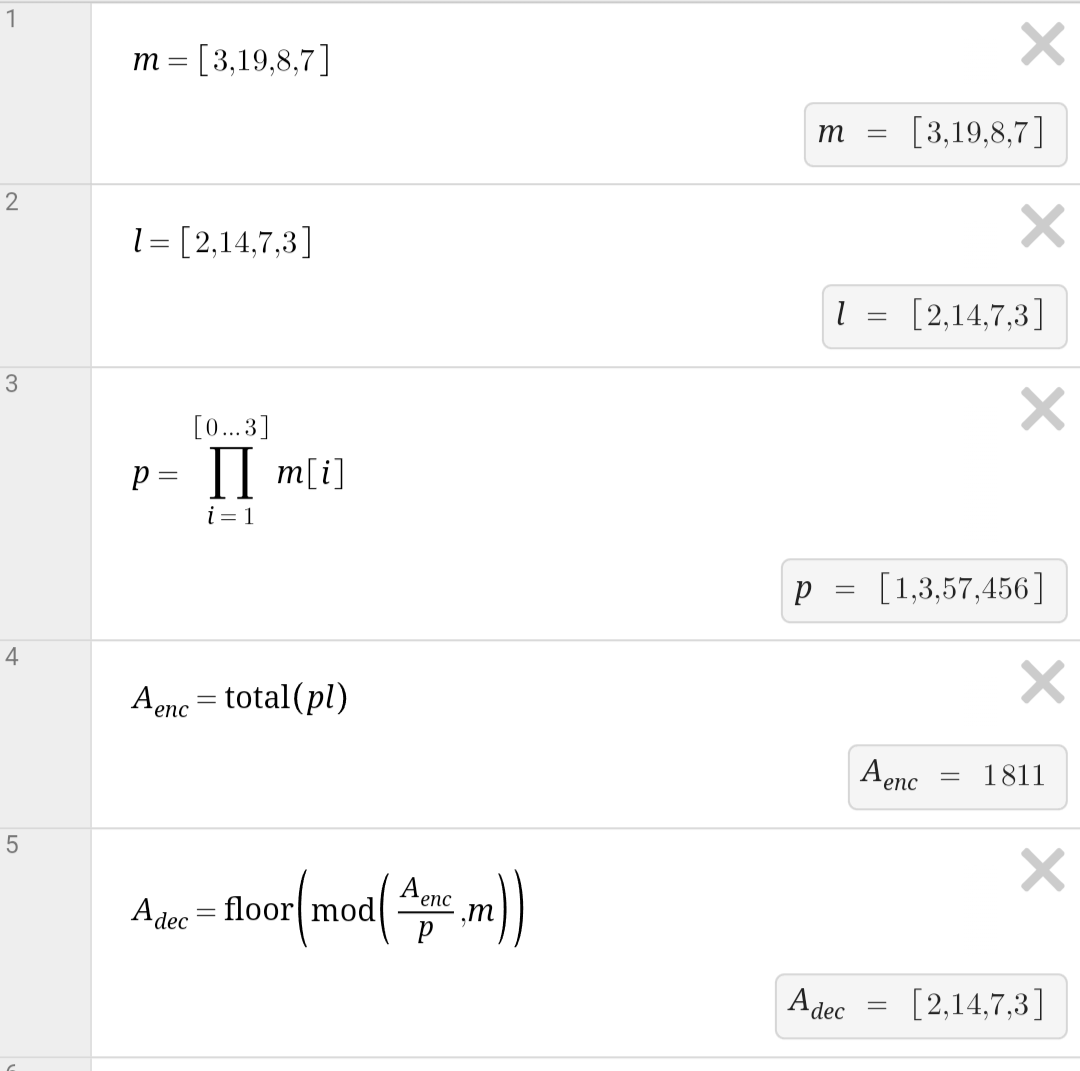
This implementation is faster and more powerful than my python implementation, as it can extract individual pieces of information just by selecting one element of the p list in the last expression. You can find a replica graph here. I recommend using ronwnor's implementation rather than mine for extracting individual pieces of data.

Repository Link