In this post, we will look at how to solve the famous Frozen Lake environment using a reinforcement learning (RL) method known as cross-entropy.
Frozen Lake is an OpenAI Gym environment in which an agent is rewarded for traversing a frozen surface from a start position to a goal position without falling through any perilous holes in the ice.
The environment is extremely simple and makes use of only discrete action and observation spaces, which we can evaluate using the following code:
import gym
env = gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False)
print(f"Action space: {env.action_space}")
print(f"Observation space: {env.observation_space}")Action space: Discrete(4)
Observation space: Discrete(16)The Discrete(4) action space indicates we can control our agent in one of four ways using integers between 0 and 3. The Frozen Lake documentation tells us that these integers correspond to the following actions:
- 0: LEFT
- 1: DOWN
- 2: RIGHT
- 3: UP
Similarly, the Discrete(16) observation space means there are 16 different states represented by integers between 0 and 15. From the documentation, the 16 states correspond to the agent's position on a map encoded using current_row * number_of_rows + current_column where both the row and column start at 0.
The state when the agent reaches the goal position in the bottom right hand corner of the 4x4 map is therefore calculated as: (3 * 4) + 3 = 15.
The reward structure is super simple: +1 for reaching the end goal and 0 for any other position including holes in the ice. The highest total reward for a successful episode is therefore 1.
Equipped with this information, we can begin to prepare our cross-entropy solution. We will use the following steps:
- Create a neural network
- Use the neural network to play a batch of episodes using the states as inputs and the outputs as actions
- Set a reward threshold and filter out "bad" episodes that have episode rewards below the threshold
- Train the neural network on the remaining "good" episodes using the states as inputs and the actions taken as desired outputs; our objective will be to minimise the loss between the neural network output and the desired output
- Repeat from step 2 until the mean episode reward of a batch is good enough
The most important parts of the solution are described below, and a complete copy of the source code is included at the end of this post and in my frozen-lake-rl repository.
For step 1, we will create a very simple neural network using PyTorch that has a single hidden layer with ReLu activation and 128 neurons.
Before we get into the code, we should work out how we can feed the state into our neural network; this is required in steps 2 and 4. We saw above that the state is an integer with 16 possible values between 0 and 15. In our case, this is not be an ideal input for our neural network. Why? Because our neural network may interpret larger values as better than smaller values or vice versa. This would be fine if the state represented a variable with natural ordering such as speed or temperature but here it does not; it simply reflects the agent's position.
The remedy is to one hot encode the state integer into a list of 16 float numbers where all of the numbers are zero except for a 1.0 in the index that corresponds to the value of the integer.
With this approach, a state of 2, for example, would be represented by:
[0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
The simplest way to one hot encode the state within our solution is to leverage the built-in support for Gym observation wrappers. The code below will create an environment in the usual way and then apply the one hot encoding wrapper to it.
class DiscreteOneHotWrapper(gym.ObservationWrapper):
def __init__(self, env):
super(DiscreteOneHotWrapper, self).__init__(env)
self.observation_space = gym.spaces.Box(0.0, 1.0, (env.observation_space.n, ), dtype=np.float32)
def observation(self, observation):
res = np.copy(self.observation_space.low)
res[observation] = 1.0
return res
env = DiscreteOneHotWrapper(gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False))Our neural network will have 16 inputs to accept the one hot encoded state and 4 outputs. The outputs will represent an unnormalised probability distribution over the four possible actions.
Ordinarily, we would use a softmax activation to normalise the outputs and thus make them add up to one. We don’t here because our CrossEntropyLoss loss function expects the unnormalised, raw values. Instead, we just need to remember to apply softmax as a separate function when using our neural network outside of training.
HIDDEN_SIZE = 128
LEARNING_RATE = 0.001
class NeuralNet(nn.Module):
def __init__(self, obs_size, hidden_size, n_actions):
super(NeuralNet, self).__init__()
self.net = nn.Sequential(
nn.Linear(obs_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, n_actions)
)
def forward(self, x):
return self.net(x)
net = NeuralNet(observation_shape, HIDDEN_SIZE, actions_n)
objective = nn.CrossEntropyLoss()
optimiser = optim.Adam(params=net.parameters(), lr=LEARNING_RATE)To train our neural network and monitor progress, we need a mechanism for recording information about each episode. We will do this by defining two named tuples, Episode and EpisodeStep:
Episode = namedtuple('Episode', ['reward', 'reward_with_discount', 'steps'])
EpisodeStep = namedtuple('EpisodeStep', ['state', 'action'])Our solution will be orchestrated by a training loop. The loop will iterate batches of episodes that have been created using a generator function called generate_batches_of_episodes.
Each time we process a batch, we will calculate the mean episode reward and use that value to determine whether the environment has been solved. We will look for a mean episode reward of more than 0.8. This translates to more than 8 in every 10 episodes within a batch reaching the goal position.
BATCH_SIZE = 100
PERCENTILE = 30
GAMMA = 0.9
best_episodes_memory = []
# Generate batches of episodes and iterate a batch at a time
for iteration, batch in enumerate(generate_batches_of_episodes(env, net, BATCH_SIZE, actions_n)):
mean_episode_reward = float(np.mean(list(map(lambda s: s.reward, batch))))
mean_episode_reward_with_discount = float(np.mean(list(map(lambda s: s.reward_with_discount, batch))))
# Check the mean reward within the batch
if mean_episode_reward > 0.8:
print("Environment solved!")
breakEarly on, because our neural network is intialised with random weights and biases, the mean episode reward will be very low. To increase the mean, we need to carry out the filtering and training steps of the cross-entropy method defined in steps 3 and 4.
To do this, we will filter out the episodes in a batch with the worst rewards using the filter_batch function. The function will return tensors for the states and actions in the current batch that resulted in the best rewards, and also a list called best_episodes_memory containing Episode objects with high rewards from earlier batches. Using new and recent sources of high performing Episode objects will help to speed up training.
# Filter the batch and retain the best states and actions for training
best_episodes_memory, batch_states_t, batch_actions_t, episode_reward_threshold = filter_batch(best_episodes_memory+batch, PERCENTILE)Next, we will train our neural network using the batch_states_t tensor as the input. The objective will be to minimise the cross entropy loss between our neural network's output and the batch_actions_t tensor. In other words, our neural network will gradually align with recommending the actions that we know lead to good rewards.
# Skip this iteration if we don't have any data to train on
if not best_episodes_memory:
continue
# Train the neural network
optimiser.zero_grad()
action_predictions = net(batch_states_t)
loss = objective(action_predictions, batch_actions_t)
loss.backward()
optimiser.step()This completes the training loop. We should expect to iterate several times - taking a batch of episodes, filtering it and using it for training - before the mean episode reward is high enough to deem the environment solved.
Let's drill-down into the two functions that are called by the training loop, starting with generate_batches_of_episodes. The purpose of this function is to carry out episodes and perform actions within each episode, before yielding them to the training loop in a list of Episode objects.
We will use the Numpy random.choice method to choose an action. The expression below will generate a random number between 0 and 3 based on the probabilities from our neural network for each of the four possible actions.
Our use of the random.choice method in this way will provide just enough randomness to balance further exploration of the environment with exploiting the actions we know lead to good rewards.
episode_reward = 0.0
episode_steps = []
batch = []
sm = nn.Softmax(dim=1)
# Reset the environment and capture the current state
state, _ = env.reset()
while True:
# Use the neural network with random.choice to choose an action
state_t = torch.FloatTensor([state])
action_probs_t = sm(net(state_t))
action_probs = action_probs_t.data.numpy()[0]
action = np.random.choice(actions_n, p=action_probs)To understand the operation of the last four lines above, consider that we start with a discrete state of 1. In this scenario, our observation wrapper will one hot encode the state as:
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]Before we can pass the state to our neural network, we need to convert it to a tensor. We do this using the torch.FloatTensor method to create state_t:
tensor([[0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]])Next, we pass state_t into our neural network and then into the softmax function to return a tensor a called action_probs_t containing a normalised probability distribution for the four actions:
tensor([[0.2629, 0.2868, 0.2318, 0.2185]], grad_fn=<SoftmaxBackward0>)We decode it from a tensor into a NumPy array:
[0.26288426 0.28681505 0.23181237 0.21848825]And finally, we choose an action using random.choice and the probabilities output from our neural network. In this example, the suggested action is 2 which corresponds with a step that moves our agent to the right.
2Still in the generate_batches_of_episodes function, the next part of the code will carry out the step, capture the reward and then add an EpisodeStep object containing the state and action to a list:
# Apply a step using the chosen action
next_state, reward, terminated, truncated, _ = env.step(action)
# Add the reward to the total reward for this episode
episode_reward += reward
# Record the state before the action was taken and the action itself
episode_steps.append(EpisodeStep(state=state, action=action))When the episode is terminated (goal or hole reached) or truncated (too many steps taken), we will wrap up the episode by adding the list of EpisodeStep objects to an Episode object along with the episode reward and a discounted version of the episode reward. The discount will help to provide variability in the reward and uses GAMMA and the number of episode steps to achieve this.
When enough episodes have been gathered, the function returns the list of Episode objects to the training loop using the yield command. When the training loop later hands back to this function, it will continue executing from the line immediately after the yield:
# Check if the episode has ended
if terminated or truncated:
# Discount the total episode reward to create variability between episodes
episode_reward_with_discount = episode_reward * (GAMMA ** len(episode_steps))
# Record the episode
batch.append(Episode(reward=episode_reward, reward_with_discount=episode_reward_with_discount, steps=episode_steps))
# Reset vars
episode_reward = 0.0
episode_steps = []
next_state, _ = env.reset()
if len(batch) == batch_size:
# Return the batch to the training loop
yield batch
batch = []
state = next_stateWe now move onto the code for the filter_batch function. The purpose of this function is to remove episodes within a batch that have a reward below a threshold.
When it comes to defining the threshold, we can exploit the variability in the discounted episode reward since it will provide a spread of values rather than just the 1 or 0 we have with the standard episode reward.
In our case, we will use the NumPy percentile method to deduce the q-th percentile from the list of discounted episode rewards, where q is PERCENTILE. We will then assign the result to episode_reward_threshold.
We will then iterate through each episode in a batch and only retain it if its discounted episode reward is above the threshold that we have just deduced.
Note, a batch may also include the best episodes from earlier batches so we will limit the number of filtered episodes that we return to 500 using best_episodes[-500:]:
# Set a threshold based on the n-th percentile of discounted episode rewards within the batch
episode_reward_threshold = np.percentile(list(map(lambda s: s.reward_with_discount, batch)), percentile)
best_episodes = []
batch_states = []
batch_actions = []
for episode in batch:
if episode.reward_with_discount > episode_reward_threshold:
# Add the states and actions from a high performing episode
batch_states.extend(map(lambda step: step.state, episode.steps))
batch_actions.extend(map(lambda step: step.action, episode.steps))
best_episodes.append(episode)
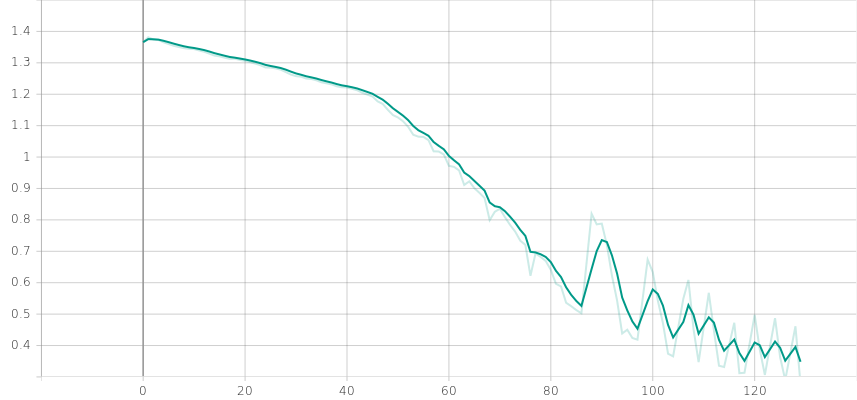
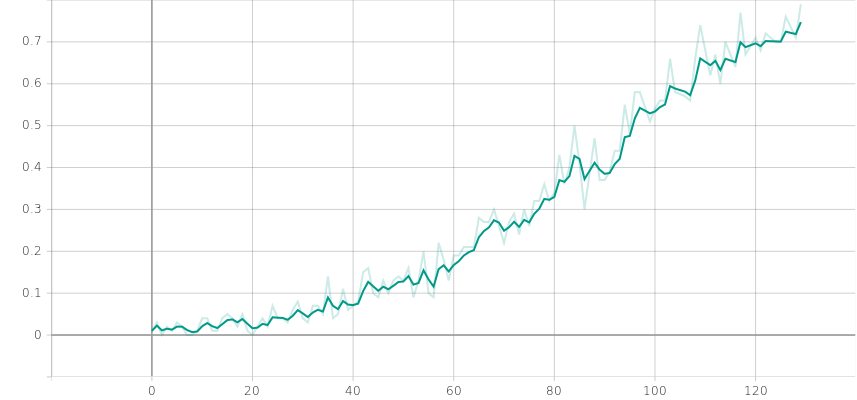
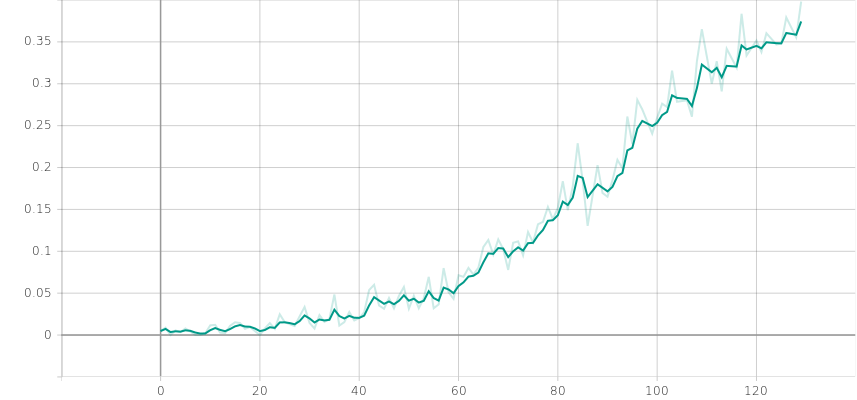
return best_episodes[-500:], torch.FloatTensor(batch_states), torch.LongTensor(batch_actions), episode_reward_thresholdRunning the code leads to a solution being found after around 120 episodes:
0: Loss: 1.3657 Mean ep reward: 0.01 Mean disc ep reward: 0.0048
1: Loss: 1.3814 Mean ep reward: 0.03 Mean disc ep reward: 0.0088
2: Loss: 1.3742 Mean ep reward: 0.0 Mean disc ep reward: 0.0
3: Loss: 1.3726 Mean ep reward: 0.02 Mean disc ep reward: 0.0055
4: Loss: 1.3654 Mean ep reward: 0.01 Mean disc ep reward: 0.0035
5: Loss: 1.3597 Mean ep reward: 0.03 Mean disc ep reward: 0.0078
6: Loss: 1.3542 Mean ep reward: 0.02 Mean disc ep reward: 0.0042
7: Loss: 1.3504 Mean ep reward: 0.0 Mean disc ep reward: 0.0
8: Loss: 1.3466 Mean ep reward: 0.0 Mean disc ep reward: 0.0
9: Loss: 1.3447 Mean ep reward: 0.01 Mean disc ep reward: 0.0021
10: Loss: 1.3438 Mean ep reward: 0.04 Mean disc ep reward: 0.0116
11: Loss: 1.3393 Mean ep reward: 0.04 Mean disc ep reward: 0.0122
12: Loss: 1.3352 Mean ep reward: 0.01 Mean disc ep reward: 0.0028
13: Loss: 1.3291 Mean ep reward: 0.01 Mean disc ep reward: 0.0023
14: Loss: 1.323 Mean ep reward: 0.04 Mean disc ep reward: 0.011
...
...
...
111: Loss: 0.5678 Mean ep reward: 0.62 Mean disc ep reward: 0.3
112: Loss: 0.4479 Mean ep reward: 0.67 Mean disc ep reward: 0.3268
113: Loss: 0.3356 Mean ep reward: 0.6 Mean disc ep reward: 0.2909
114: Loss: 0.3315 Mean ep reward: 0.7 Mean disc ep reward: 0.3418
116: Loss: 0.4725 Mean ep reward: 0.64 Mean disc ep reward: 0.3193
117: Loss: 0.3119 Mean ep reward: 0.77 Mean disc ep reward: 0.3836
118: Loss: 0.3133 Mean ep reward: 0.67 Mean disc ep reward: 0.3338
120: Loss: 0.4974 Mean ep reward: 0.71 Mean disc ep reward: 0.3516
121: Loss: 0.3878 Mean ep reward: 0.68 Mean disc ep reward: 0.3379
122: Loss: 0.3064 Mean ep reward: 0.72 Mean disc ep reward: 0.3603
124: Loss: 0.4871 Mean ep reward: 0.7 Mean disc ep reward: 0.3469
125: Loss: 0.3627 Mean ep reward: 0.7 Mean disc ep reward: 0.3479
126: Loss: 0.2901 Mean ep reward: 0.76 Mean disc ep reward: 0.3791
128: Loss: 0.4612 Mean ep reward: 0.71 Mean disc ep reward: 0.3554
129: Loss: 0.2774 Mean ep reward: 0.79 Mean disc ep reward: 0.3982
Environment solved!
Loss by iteration
Mean episode reward by iteration
Mean discounted episode reward
In this post, we worked out how to solve the famous Frozen Lake environment using the cross-entropy.
Interestingly, this approach is not so effective with the non-slippery version (is_slippery=True). The mean episode reward peaks at around 0.5. To solve this scenario and indeed more complex environments, other methods can be used including value iteration, Q-learning and deep Q-networks.
For more information about all of these, I highly recommend Deep Reinforcement Learning Hands-On by Maxim Lapan; parts of the code above were inspired by the book.
Download from GitHub cross-entropy-rl repository
import random
from collections import namedtuple
import gym
import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
HIDDEN_SIZE = 128
LEARNING_RATE = 0.001
BATCH_SIZE = 100
PERCENTILE = 30
GAMMA = 0.9
Episode = namedtuple('Episode', ['reward', 'reward_with_discount', 'steps'])
EpisodeStep = namedtuple('EpisodeStep', ['state', 'action'])
class DiscreteOneHotWrapper(gym.ObservationWrapper):
def __init__(self, env):
super(DiscreteOneHotWrapper, self).__init__(env)
self.observation_space = gym.spaces.Box(0.0, 1.0, (env.observation_space.n, ), dtype=np.float32)
def observation(self, observation):
res = np.copy(self.observation_space.low)
res[observation] = 1.0
return res
class NeuralNet(nn.Module):
def __init__(self, obs_size, hidden_size, n_actions):
super(NeuralNet, self).__init__()
self.net = nn.Sequential(
nn.Linear(obs_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, n_actions)
)
def forward(self, x):
return self.net(x)
def generate_batches_of_episodes(env, net, batch_size, actions_n):
episode_reward = 0.0
episode_steps = []
batch = []
sm = nn.Softmax(dim=1)
# Reset the environment and capture the current state
state, _ = env.reset()
while True:
# Use the neural network with random.choice to choose an action
state_t = torch.FloatTensor([state])
action_probs_t = sm(net(state_t))
action_probs = action_probs_t.data.numpy()[0]
action = np.random.choice(actions_n, p=action_probs)
# Apply a step using the chosen action
next_state, reward, terminated, truncated, _ = env.step(action)
# Add the reward to the total reward for this episode
episode_reward += reward
# Record the state before the action was taken and the action itself
episode_steps.append(EpisodeStep(state=state, action=action))
# Check if the episode has ended
if terminated or truncated:
# Discount the total episode reward to create variability between episodes
episode_reward_with_discount = episode_reward * (GAMMA ** len(episode_steps))
# Record the episode
batch.append(Episode(reward=episode_reward, reward_with_discount=episode_reward_with_discount, steps=episode_steps))
# Reset vars
episode_reward = 0.0
episode_steps = []
next_state, _ = env.reset()
if len(batch) == batch_size:
# Return the batch to the training loop
yield batch
batch = []
state = next_state
def filter_batch(batch, percentile):
# Set a threshold based on the n-th percentile of discounted episode rewards within the batch
episode_reward_threshold = np.percentile(list(map(lambda s: s.reward_with_discount, batch)), percentile)
best_episodes = []
batch_states = []
batch_actions = []
for episode in batch:
if episode.reward_with_discount > episode_reward_threshold:
# Add the states and actions from a high performing episode
batch_states.extend(map(lambda step: step.state, episode.steps))
batch_actions.extend(map(lambda step: step.action, episode.steps))
best_episodes.append(episode)
return best_episodes[-500:], torch.FloatTensor(batch_states), torch.LongTensor(batch_actions), episode_reward_threshold
def render_n_steps(env, net, steps_n):
sm = nn.Softmax(dim=1)
state, _ = env.reset()
for i in range(steps_n):
state_t = torch.FloatTensor([state])
if net is None:
# Choose a random step
action = env.action_space.sample()
else:
# Choose a step using the (trained) neural network
action_probs_t = sm(net(state_t))
action = np.argmax(action_probs_t.data.numpy()[0])
state, reward, terminated, truncated, _ = env.step(action)
# Render the step on the display
env.render()
if terminated or truncated: state, _ = env.reset()
if __name__ == "__main__":
# Render random steps before training
env = DiscreteOneHotWrapper(gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False, render_mode="human"))
render_n_steps(env, None, 50)
# Create the environment
env = DiscreteOneHotWrapper(gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False))
# Capture environment information
observation_shape = env.observation_space.shape[0]
actions_n = env.action_space.n
# Create the neural network
net = NeuralNet(observation_shape, HIDDEN_SIZE, actions_n)
objective = nn.CrossEntropyLoss()
optimiser = optim.Adam(params=net.parameters(), lr=LEARNING_RATE)
best_episodes_memory = []
# Generate batches of episodes and iterate a batch at a time
for iteration, batch in enumerate(generate_batches_of_episodes(env, net, BATCH_SIZE, actions_n)):
mean_episode_reward = float(np.mean(list(map(lambda s: s.reward, batch))))
mean_episode_reward_with_discount = float(np.mean(list(map(lambda s: s.reward_with_discount, batch))))
# Check the mean reward within the batch
if mean_episode_reward > 0.8:
print("Environment solved!")
break
# Filter the batch and retain the best states and actions for training
best_episodes_memory, batch_states_t, batch_actions_t, episode_reward_threshold = filter_batch(best_episodes_memory+batch, PERCENTILE)
# Skip this iteration if we don't have any data to train on
if not best_episodes_memory:
continue
# Train the neural network
optimiser.zero_grad()
action_predictions = net(batch_states_t)
loss = objective(action_predictions, batch_actions_t)
loss.backward()
optimiser.step()
# Report performance
print(f"{iteration}:\tLoss: {round(loss.item(), 4)}\tMean ep reward: {round(mean_episode_reward, 4)}\tMean ep reward with disc: {round(mean_episode_reward_with_discount, 4)}")
# Render some steps after training
env = DiscreteOneHotWrapper(gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False, render_mode="human"))
render_n_steps(env, net, 50)
# Destroy environment
env.close()