README.Rmd

---
title: "piececor"
output: 
  github_document:
    includes:
      in_header: header.md
    toc: true
---

<!-- README.md is generated from README.Rmd. Please edit that file -->

```{r, include = FALSE}
knitr::opts_chunk$set(
  collapse = TRUE,
  comment = "#>",
  fig.path = "man/figures/README-",
  out.width = "100%"
)
```

<!-- badges: start -->
<!-- badges: end -->

piececor is a toy package for calculating piecewise correlations of a set of {*variables of interest*} with a {*target*} variable. This may be useful for exploratory data analysis or in "simple filtering" of features for predictive modeling.

This package is a *rough* mock-up of initial ideas discussed between Bryan Shalloway, Dr. Shaina Race, and Ricky Tharrington.

# Steps

The core function is `piecewise_cors()` which, for each {*variable of interest*}:

1. Splits observations into segments based on the local minima / maxima of a smoother fit on *{target} ~ {variable of interest}*.
1. Calculates the correlation between *{target} & {variable of interest}* for each segment
1. Allows for calculating a weighted correlation coefficient across segments
1. Repeat for all {*variables of interest*} with {*target*}

# Example

Use a version of `mtcars` data with some numeric columns converted to factors.
```{r, warning=FALSE, message=FALSE}
library(tidyverse)
library(piececor)

min_unique_to_fact <- function(x, min_unique = 8){
  if( (length(unique(x)) < min_unique) & is.numeric(x) ){
    return(as.factor(x))
  } else x
}

mtcars_neat <- mtcars %>%
  as_tibble(rownames = "car") %>%
  mutate(across(where(is.numeric), min_unique_to_fact))
```

## Correlations of segments

Specify `data`, `.target`, and `...`^[*variables of interest* are represented by `...` in the function.]

```{r}
mods_cors <- piecewise_cors(data = mtcars_neat,
                            .target = hp,
                            mpg, disp, drat, wt, qsec)
```

Note that [tidy selectors](https://dplyr.tidyverse.org/reference/dplyr_tidy_select.html) can be used in place of explicitly typing each *variable of interest*. I.e. in the above example `mpg, disp, drat, wt, qsec`could be replaced by `where(is.double)`.

`piecewise_cors()` returns a named list of `mods` and `cors`.

**Correlations:**

For each *variable of interest*, `cors` has a dataframe with information on the domain (`gtoe` to `lt`) for each segment of observations (`data`), the number of observations (`n_obs`) in the segment, and the associated correlation (`cor`) of the variable with `.target`.

(`cors` dataframes with one row represent smoothed fits with no local minima / maxima.)
```{r}
mods_cors$cors
```

By default `piecewise_cors()` uses Spearman's Rank Correlation Coefficient^[So is measuring the extent to which the relationship is monotonic.].

**Smoothing models:**

For each *variable of interest*, `mods` contains a [parsnip](https://github.com/tidymodels/parsnip) fit object (the smoothing model). The local minima / maxima of these fitted models determines the breakpoints for segmenting observations for each correlation calculation^[`mods` is primarily saved simply for use with `piececor::plot_splits()`.]. In our example, these may be accessed with `mods_cors$mods`.

By default `mgcv::gam()` (via a parsnip interface) is the engine for the smoother. At present, it is also the only model type that will work^[In theory, with some changes, other model types with parsnip interfaces could be added with minimal effort].

## Plots of splits

To review the split points, the outputs from `piecewise_cors()` can be passed into `plot_splits()`. *Variables of interest* that you wish to plot must be typed or specified by a tidy selector.

```{r}
mods_cors %>% 
  plot_splits(mpg, qsec)
```

To view plots for all *variables of interest*, replace `mpg, qsec` with `everything()`.

## Weighted correlation

The output from `piecewise_cors()` can be passed to the helper `weighted_abs_mean_cors()` to calculate an overall weighted "correlation" between 0 and 1 for each *variable of interest*.

```{r}
weighted_cors <- weighted_abs_mean_cors(mods_cors)

weighted_cors

weighted_cors %>% 
  mutate(name = forcats::fct_reorder(name, value)) %>% 
  ggplot(aes(y = name, x = value))+
  geom_col()+
  xlim(c(0, 1))+
  labs(title = "Weighted correlation with 'hp'")
```

By default a [Fisher transformation](https://en.wikipedia.org/wiki/Fisher_transformation) is applied to the individual correlations when calculating the weighted correlation. See `?weighted_abs_mean_cors` for more information.

See the end of section [Correlation metric] for an example calculating a p-value on piecewise correlations.

# Customizing

Arguments `custom_model_spec` and `fit_formula` can be used to customize the [Smoother fit]. `cor_function` allows for changes in the [Correlation metric] calculated on the segments. See `?piecewise_cors` for more detail on these arguments.

## Smoother fit

`custom_model_spec` can take in a parsnip model specifications^[Again only generative additive models via the "mgcv" engine may be specified. This is in large part due to a dependency on the deprecated `fderiv()` function in [gratia](https://gavinsimpson.github.io/gratia/). Though changes would also need to be made to the `fit_formula` argument in `piececor::piecewise_cors()` to accommodate this. Other non-linear, continuous models would be possible candidates, e.g. loess or multi-adaptive regression splines (which also already has a parsnip interface).]. For example, setting `sp` (smoothing parameter) to `sp = 2` gives a smoother fit to `hp ~ qsec` that no longer segments the observations:

```{r}
mod_spec <- parsnip::gen_additive_mod() %>%
  parsnip::set_engine("mgcv", method = "REML", sp = 2) %>%
  parsnip::set_mode("regression")

mods_cors_custom <- 
  piecewise_cors(data = mtcars_neat,
                 .target = hp,
                 mpg, disp, drat, wt, qsec,
                 custom_model_spec = mod_spec)

mods_cors_custom %>% 
  plot_splits(qsec)
```

Equivalently, this may be specified by passing the parameter into the `fit_formula` argument:

```{r, eval = FALSE}
# Chunk not evaluated
piecewise_cors(
  data = mtcars_neat,
  .target = hp,
  mpg, disp, drat, wt, qsec,
  fit_formula = ".target ~ s(..., sp = 2)"
)
```

See [Generalized additive models via mgcv](https://parsnip.tidymodels.org/reference/details_gen_additive_mod_mgcv.html) and associated reference pages for more details on parsnip interfaces.

## Correlation metric

Say you want to measure Pearson's rather than Spearman's correlation coefficient on segments, you could use the `cor_function` argument to change the lambda function:
```{r}
piecewise_cors(
  data = mtcars_neat,
  .target = hp,
  mpg, disp, drat, wt, qsec,
  cor_function = "~cor(.x, method = 'pearson')[2,1]"
) %>%
  weighted_abs_mean_cors()
```

You aren't prevented from passing into `cor_function` lambda functions^[*Character strings of tidyverse shortcut syntax for lambda functions.] to calculate metrics/statistics other than correlations^[Provided the lambda function evaluates to a numeric vector of length 1]. 

For example, say we want to see the p.value's of Pearson correlations^[Used Pearson rather than Spearman in this example because Spearman can more easily get odd cases where end-up with p-values of 1, which happens in this case, and break common methods for combining p-values] at each segment for `hp ~ qsec`:

```{r, warning=FALSE}
# Warnings silenced in chunk output
mods_cors_pvalues <- 
  piecewise_cors(data = mtcars_neat,
                 .target = hp,
                 mpg, disp, drat, wt, qsec,
# cor.test() expects x and y vectors not a matrix or dataframe
                 cor_function = "~cor.test(.x[[1]], .x[[2]], method = 'pearson')$p.value"
  )

# let's check for qsec
mods_cors_pvalues$cors$qsec
```

The `cor` column here actually represents the statistical test (run separately on each segment) of the null hypothesis that the correlation coefficient is 0.

We could use Stouffer's [Z-score method](https://en.wikipedia.org/wiki/Fisher%27s_method#Relation_to_Stouffer's_Z-score_method) to combine these into an overall p-value:

```{r}
# combine_test() is (mostly) copied from {survcomp} package
mods_cors_pvalues$cors$qsec %>% 
  with(piececor:::combine_test(cor, n_obs, method = "z.transform"))
```

# Installation

Install from github with:

```{r, eval = FALSE}
devtools::install_github("brshallo/piececor")
```

# Limitations & Notes

* Very slow compared to other common "simple filtering" methods for predictive modeling^[Given that for each *variable of interest* an `mgcv` model is fit -- along with various other steps.].
* Trying on a few different datasets, it often does not pass the "eye test". 
    * Splits often come near flatter parts of the data or at the tails of the distribution where there are fewer points
* {piececor} is intended for when trying to measure non-linear and *non-monotonic* associations. If the relationships are likely monotonic, generally using either Spearman's or Kendall's correlation coefficients is a better + faster option^[].
* Changing default correlation method from Spearman's to Kendall's probably makes sense (as Kendall's has better statistical properties -- particularly regarding calculating p-values), though I should verify that Fisher's transformation can also be used with Kendall's method^[See [MoseleyBioinformaticsLab/ICIKendallTau](https://t.co/5BGfmiNgG4?amp=1) for a faster implementation of Kendall's method than offered in the `cor(x, method = "kendall")` approach in the base R stats package.].
* Output of `weighted_abs_mean_cors()` is not particularly meaningful in a traditional notion of "correlation."
    * Splits are determined based on optimizing a fit to a {*target*} -- therefore flipping *{target} ~ {variable of interest}* to *{variable of interest} ~ {target}* produces different weighted correlation scores^[Correlation measures usually don't have some notion of a target, so the measures would be the same.]. A smoother that was fit based on total least squares or minimizing orthogonal distance or some other approach may be more appropriate.
* How to do weighted correlation metrics and associated p-values generally should be given a bit more thought.
    * Other resources on "simple filtering" techniques (e.g. from [Feature Engineering and Selection...](http://www.feat.engineering/greedy-simple-filters.html)) recommend converting scores of feature importance to some standardized metric, e.g. a p-value.    
* There is extensive literature in predictive modeling on identifying *knots*. The experiment with this package is to take advantage of existing software that uses knots or other smoothing techniques and then instead to consider the local minima / maxima created by those techniques to inform cut-points. The defaults of "mgcv" hopes to prevent overfitting and the use of "Spearman's" correlation means we're checking whether the relationship is monotonic. 
    * However we haven't done a ton of research on relevant literature concerning knots and other methods for determining cut-points.
    * Right now the cut-points are essentially determined by looking where in the smoothed fits the first derivative == 0. We may want to consider critical points or other methods. We may also want to have some level of tolerance or requisite change in slope or observations in segment, etc. so that minor bumps don't create multiple segments.
* `custom_model_spec` allows a parsnip model specification, with the idea that this would facilitate the input of any kind of smoother supported by parsnip (e.g. MARS, polynomial regression, ...). However actually implementing this would require the removal of the dependency on [gratia](https://gavinsimpson.github.io/gratia/) as well as multiple other changes to piececor.
* More thought should go into the structure of the output of `piecewise_cors()`
* (Almost) no checks, tests, catches, etc. have been set-up

# Resources

Links are copied from slack discussions^[And not properly cited] and may be only tangentially related to piececor package. 

* Within the [easystats](https://github.com/easystats) ecosystem is the [correlation](https://easystats.github.io/correlation/articles/types.html) package / function that supports [Distance correlation](https://en.wikipedia.org/wiki/Distance_correlation) that measures both linear and non-linear associations.
* The [infotheo](https://github.com/affeldt-aist/infotheo) package supports measuring the amount of [mutual information](https://en.wikipedia.org/wiki/Mutual_information) between variables.
* [NNS](https://github.com/OVVO-Financial/NNS) Package for Nonlinear nonparametric statistics, related to kernel regression techniques (python package also available).
* [ppsr](https://github.com/paulvanderlaken/ppsr) R implementation of predictive power score which outputs a normalized score of how well x predicts y (using a particular model specification and choice of performance metric) -- python package is also available.
* [ProcessMiner/nlcor](https://github.com/ProcessMiner/nlcor) package (non-linear correlation)[^nlcor].

I ran a rough speed test on these methods [here](https://gist.github.com/brshallo/6087347f5572feecbb7fa5cbd5e4a8fa):

![speed test of various methods, mutual information is the fastest.](https://pbs.twimg.com/media/FCQmvR1UcAA-98I?format=png&name=small)

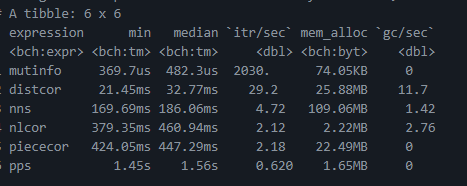
* See [gist](https://gist.github.com/brshallo/6087347f5572feecbb7fa5cbd5e4a8fa) for speed tests on above packages and piececor.
* For tidy interface for measures of association also see [infer](https://github.com/tidymodels/infer),  [corrr](https://corrr.tidymodels.org/), [easystats](https://github.com/easystats/easystats)
* Just *slightly* tangential, there are a ton of non-linear projection methods out there, e.g. KPCA, UMAP, ICA, tSNE, and many others... many of these are accessible via recipes or embed packages in tidymodels ecosystem.
* "Variable Importance Analysis: A Comprehensive review" https://www.sciencedirect.com/science/article/abs/pii/S0951832015001672
* "Permutation importance: a corrected feature importance measure" https://academic.oup.com/bioinformatics/article/26/10/1340/193348?login=true
* "A computationally fast variable importance test for random
forests for high-dimensional data" https://core.ac.uk/download/pdf/216462194.pdf
* ELI5 python package: https://eli5.readthedocs.io/en/latest/overview.html#basic-usage
* "How To Assess Statistical Significance In Your Data with Permutation Tests" https://towardsdatascience.com/how-to-assess-statistical-significance-in-your-data-with-permutation-tests-8bb925b2113d
* "Interpretable Machine Learning" https://christophm.github.io/interpretable-ml-book/
* Getting derivitives from GAM's
    * https://gavinsimpson.github.io/gratia/reference/fderiv.html 
    * https://stackoverflow.com/questions/14207250/determining-derivatives-from-gam-smooth-object 
* Covariant Derivatives https://en.wikipedia.org/wiki/Covariant_derivative
* "Efficient test for nonlinear dependence of two continuous variables" https://bmcbioinformatics.biomedcentral.com/articles/10.1186/s12859-015-0697-7
* 11.2 Simple Filters, from Feature Engineering and Selection... http://www.feat.engineering/greedy-simple-filters.html
* Fisher transformation https://en.wikipedia.org/wiki/Fisher_transformation
* Parsnip package documentation on generalized additive models: https://parsnip.tidymodels.org/reference/details_gen_additive_mod_mgcv.html


[^nlcor]:  
    
    * nlcor uses Pearson correlation whereas piececor defaults to use Spearman, with the option of overriding this with `cor_function` argument
    * nlcor uses adaptive local linear correlation computations to determine cut-points whereas piececor uses the local maxima / minima of a smoother defined by a {`parsnip`} model specification. 
    * nlcor currently does not apply any transformations when calculating 'total adjusted' correlations and associated p-values (see [github comment](https://github.com/ProcessMiner/nlcor/issues/15#issuecomment-928320054)).